题目内容
8.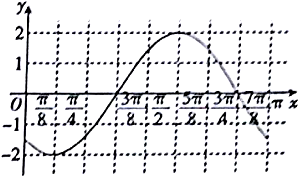 函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ=$\frac{π}{4}$.
函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ=$\frac{π}{4}$.
分析 由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,可得f(x)的解析式.再利用y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,结合条件,利用正弦函数的定义域和值域,求得θ的值..
解答 解:根据函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象,
可得A=-2,$\frac{T}{4}$=$\frac{1}{4}•\frac{2π}{ω}$=$\frac{3π}{8}-\frac{π}{8}$,∴ω=2.
再根据五点法作图可得2•$\frac{3π}{8}$+φ=π,∴φ=$\frac{π}{4}$,f(x)=-2sin(2x+$\frac{π}{4}$).
将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)=-2sin(2x-$\frac{7π}{12}$+$\frac{π}{4}$)=-2sin(2x-$\frac{π}{3}$)的图象,
对于函数y=g(x),当x∈$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$),2x-$\frac{π}{3}$∈[-π,2θ-$\frac{π}{3}$],
由于g(x)的值域为[-1,2],故-2sin(2x-$\frac{π}{3}$)的最小值为-1,此时,2sin(2θ-$\frac{π}{3}$)=$\frac{1}{2}$,
则θ=$\frac{π}{4}$,
故答案为:$\frac{π}{4}$.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值.还考查y=Asin(ωx+φ)的图象变换规律,正弦函数的定义域和值域,属于中档题.

| A. | {-1,0,1} | B. | {0,1,2} | C. | {0,1,2,3} | D. | {-1,0,1,2,3} |
| A. | -2014 | B. | -2015 | C. | -2016 | D. | -2017 |
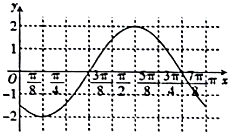 函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ等于( )
函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ等于( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{7π}{12}$ |
| A. | 甲品牌1个,乙品牌8个 | B. | 甲品牌2个,乙品牌7个 | ||
| C. | 甲品牌3个,乙品牌6个 | D. | 甲品牌4个,乙品牌5个 |
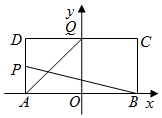 如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD的中点,且直线AQ与BP的交点在椭圆E:$\frac{x^2}{a^2}$+y2=1(a>0)上.
如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD的中点,且直线AQ与BP的交点在椭圆E:$\frac{x^2}{a^2}$+y2=1(a>0)上.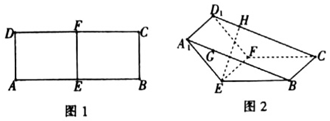 如图1,在矩形ABCD中,AB=8,AD=3,点E、F分别为AB、CD的中点,将四边形AEFD沿EF折到A1EFD1的位置,使∠A1EB=120°,如图2所示,点G,H分别在A1B,D1C上,A1G=D1H=$\sqrt{3}$,过点G,H的平面α与几何体A1EB-D1FC的面相交,交线围成一个正方形.
如图1,在矩形ABCD中,AB=8,AD=3,点E、F分别为AB、CD的中点,将四边形AEFD沿EF折到A1EFD1的位置,使∠A1EB=120°,如图2所示,点G,H分别在A1B,D1C上,A1G=D1H=$\sqrt{3}$,过点G,H的平面α与几何体A1EB-D1FC的面相交,交线围成一个正方形.