题目内容
10.医学上某种还没有完全攻克的疾病,治疗时需要通过药物控制其中的两项指标H和V.现有..三种不同配方的药剂,根据分析,A,B,C三种药剂能控制H指标的概率分别为0.5,0.6,0.75,能控制V指标的概率分别是0.6,0.5,0.4,能否控制H指标与能否控制V指标之间相互没有影响.(Ⅰ)求A,B,C三种药剂中恰有一种能控制H指标的概率;
(Ⅱ)某种药剂能使两项指标H和V都得到控制就说该药剂有治疗效果.求三种药剂中有治疗效果的药剂种数X的分布列.
分析 (Ⅰ)利用相互独立事件概率乘法公式、互斥事件概率加法公式能求出A,B,C三种药剂中恰有一种能控制H指标的概率.
(Ⅱ)求出A,B,C三种药剂有治疗效果的概率均为0.3,可看成是独立重复试验,即X~B(3,0.3),由此能求出X的分布列.
解答 解:(Ⅰ)A,B,C三种药剂中恰有一种能控制H指标的概率为:
$P=P(A\overline B\overline C)+P(\overline AB\overline C)+P(\overline A\overline BC)$
=0.5×(1-0.6)×(1-0.75)+(1-0.5)×0.6×(1-0.75)+(1-0.5)×(1-0.6)×0.75=0.275.
(Ⅱ)∵A有治疗效果的概率为PA=0.5×0.6=0.3,
B有治疗效果的概率为PB=0.6×0.5=0.3,
C有治疗效果的概率为PC=0.75×0.4=0.3,
∴A,B,C三种药剂有治疗效果的概率均为0.3,可看成是独立重复试验,即X~B(3,0.3),
∵X的可能取得为0,1,2,3,
∴$P(X=k)=C_3^k×{0.3^k}×{(1-0.3)^{3-k}}$,
即$P(X=0)=C_3^0×{0.3^0}×{(1-0.3)^3}=0.343$,
$P(X=1)=C_3^1×0.3×{(1-0.3)^2}=0.441$,
$P(X=2)=C_3^2×{0.3^2}×(1-0.3)=0.189$,
$P(X=3)=C_3^3×{0.3^3}=0.027$
故X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | 0.343 | 0.441 | 0.189 | 0.027 |
点评 本题考查概率的求法,考查离散型随机变量的分布列,考查相互独立事件概率乘法公式、互斥事件概率加法公式、二项分布等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想,是中档题.

练习册系列答案
相关题目
20.在等比数列{an}中,a1=2,公比q=2,若am=a1a2a3a4(m∈N*),则m=( )
| A. | 11 | B. | 10 | C. | 9 | D. | 8 |
15.i为虚数单位,则i+i2+i3+i4=( )
| A. | 0 | B. | i | C. | 2i | D. | -i |
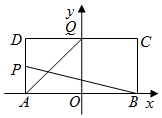 如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD的中点,且直线AQ与BP的交点在椭圆E:$\frac{x^2}{a^2}$+y2=1(a>0)上.
如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD的中点,且直线AQ与BP的交点在椭圆E:$\frac{x^2}{a^2}$+y2=1(a>0)上.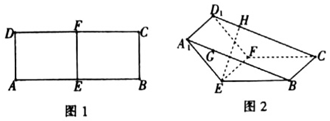 如图1,在矩形ABCD中,AB=8,AD=3,点E、F分别为AB、CD的中点,将四边形AEFD沿EF折到A1EFD1的位置,使∠A1EB=120°,如图2所示,点G,H分别在A1B,D1C上,A1G=D1H=$\sqrt{3}$,过点G,H的平面α与几何体A1EB-D1FC的面相交,交线围成一个正方形.
如图1,在矩形ABCD中,AB=8,AD=3,点E、F分别为AB、CD的中点,将四边形AEFD沿EF折到A1EFD1的位置,使∠A1EB=120°,如图2所示,点G,H分别在A1B,D1C上,A1G=D1H=$\sqrt{3}$,过点G,H的平面α与几何体A1EB-D1FC的面相交,交线围成一个正方形.