题目内容
14.已知边长为a的正方形ABCD外有一点P,且PA⊥平面ABCD,PA=a,求二面角B-PA-C和P-BC-A的大小.
分析 由已知条件推导出BC⊥平面PAB,从而得到二面角B-PA-C的大小就是∠BAC,二面角P-BC-A的平面角为∠PBA,由此能求出二面角P-BC-A的大小.
解答 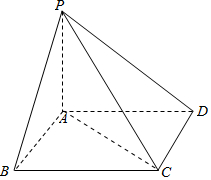 解:∵边长为a的正方形ABCD外有一点P,∵PA⊥AB,PA=AB,∴∠PBA=45°,
解:∵边长为a的正方形ABCD外有一点P,∵PA⊥AB,PA=AB,∴∠PBA=45°,
连接AC,PA⊥平面ABCD,可得AB⊥PA,
PA⊥AC,二面角B-PA-C即为∠BAC即为所求的角,为45°.
∵边长为a的正方形ABCD外有一点P,且PA⊥平面ABCD,
PA=a,又∵ABCD为正方形,∴AB⊥BC,
∵PA∩AB=A,∴BC⊥平面PAB,
∵PA?平面PAB,∴BC⊥PA,
又CD⊥BC,
∴二面角P-BC-A的平面角即为∠PBA即为所求的角,为45°.
二面角B-PA-C和P-BC-A的大小都是45°.
点评 本题考查二面角的大小的求法,是中档题,解题时要注意是思维能力的培养.

练习册系列答案
相关题目
7.已知 x>1,y>1,且 lg x,2,lg y 成等差数列,则 x+y 有( )
| A. | 最小值 20 | B. | 最小值 200 | C. | 最大值 20 | D. | 最大值 200 |
3.已知a>0,b>0,则$\frac{{a}^{2}+4+4ab+4{b}^{2}}{a+2b}$的最小值为( )
| A. | $\frac{1}{4}$ | B. | 1 | C. | 2 | D. | 4 |
4.已知α,β为平面,a,b,c为直线,下列命题正确的是( )
| A. | a?α,若b∥a,则b∥α | B. | α⊥β,α∩β=c,b⊥c,则b⊥β | ||
| C. | a⊥b,b⊥c,则a∥c | D. | a∩b=A,a?α,b?α,a∥β,b∥β,则α∥β |