题目内容
3．已知a＞0，b＞0，则$\frac{{a}^{2}+4+4ab+4{b}^{2}}{a+2b}$的最小值为（ ）| A． | $\frac{1}{4}$ | B． | 1 | C． | 2 | D． | 4 |
分析 构造基本不等式的性质即可求解．
解答 解：由$\frac{{a}^{2}+4+4ab+4{b}^{2}}{a+2b}$=$\frac{（a+2b）^{2}+4}{a+2b}=（a+2b）+\frac{4}{a+2b}$
∵a＞0，b＞0，
∴$（a+2b）+\frac{4}{a+2b}≥2\sqrt{\frac{4}{a+2b}•（a+2b）}$=4，当且仅当a+2b=2时取等号．
则$\frac{{a}^{2}+4+4ab+4{b}^{2}}{a+2b}$的最小值为4．
故选D
点评 本题考查了“构造思想”与基本不等式的性质运用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
15．
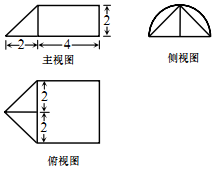某几何体的三视图如图所示，则该几何体的体积为（ ）
某几何体的三视图如图所示，则该几何体的体积为（ ）| A． | $\frac{8}{3}$+8π | B． | $\frac{16}{3}$+8π | C． | $\frac{8}{3}$+16π | D． | $\frac{16}{3}$+16π |
11．若函数f（x）=$\frac{sinx+a}{cosx}$在区间（0，$\frac{π}{2}$）上单调递增，则实数a的取值范围是（ ）
| A． | a≤-1 | B． | a≤2 | C． | a≥-1 | D． | a≤1 |
18．哈市某公司有五个不同部门，现有4名在校大学生来该公司实习，要求安排到该公司的两个部门，且每部门安排两名，则不同的安排方案种数为（ ）
| A． | 40 | B． | 60 | C． | 120 | D． | 240 |
8．记复数z的共轭复数为$\overline{z}$，若$\overline{z}$（1-i）=2i（i为虚数单位），则复数z的模|z|=（ ）
| A． | $\sqrt{2}$ | B． | 1 | C． | 2$\sqrt{2}$ | D． | 2 |
12．若sin（π-α）=$\frac{1}{3}$，且$\frac{π}{2}$≤α≤π，则cosα=（ ）
| A． | $\frac{2\sqrt{2}}{3}$ | B． | -$\frac{2\sqrt{2}}{3}$ | C． | -$\frac{4\sqrt{2}}{9}$ | D． | $\frac{4\sqrt{2}}{9}$ |