题目内容
6.函数f(x)=$\sqrt{3}$sinωxcosωx+cos2ωx(ω>0)(ω>0)在区间[$\frac{π}{6}$,$\frac{π}{3}$]的值域是[-$\frac{1}{2}$,$\frac{1}{2}$],则常数ω所有可能的值的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
分析 利用二倍角和辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,将内层函数看作整体,求出其范围,根据值域是[-$\frac{1}{2}$,$\frac{1}{2}$],建立关系,讨论常数ω所有可能的值.
解答 解:函数f(x)=$\sqrt{3}$sinωxcosωx+cos2ωx,
化简可得:f(x)=$\frac{\sqrt{3}}{2}sin2ωx+\frac{1}{2}cos2ωx+\frac{1}{2}$=sin(2ωx+$\frac{π}{6}$)$+\frac{1}{2}$,
∵x∈[$\frac{π}{6}$,$\frac{π}{3}$],f(x)∈[$-\frac{1}{2}$,$\frac{1}{2}$],
∴-1≤sin(2ωx+$\frac{π}{6}$)≤0,
则$\frac{T}{4}≤\frac{π}{3}-\frac{π}{6}≤\frac{T}{2}$,
而T=$\frac{2π}{2ω}=\frac{π}{ω}$,
那么:$\frac{π}{4ω}≤\frac{π}{6}≤\frac{π}{2ω}$,即$\frac{3}{2}≤ω≤3$.
sin(2ωx+$\frac{π}{6}$)=0的结果必然是$x=\frac{π}{6}$或$\frac{π}{3}$.
当$x=\frac{π}{6}$时,解得ω=$\frac{5}{2}$满足题意.
当x=$\frac{π}{3}$时,解得ω=$\frac{11}{4}$满足题意.
∴常数ω所有可能的值的个数为2.
故选C:
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
19.执行如图所示的程序框图,则输出S的值是( )
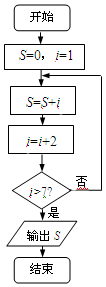

| A. | 9 | B. | 16 | C. | 25 | D. | 27 |
11.若函数f(x)=$\frac{sinx+a}{cosx}$在区间(0,$\frac{π}{2}$)上单调递增,则实数a的取值范围是( )
| A. | a≤-1 | B. | a≤2 | C. | a≥-1 | D. | a≤1 |
18.哈市某公司有五个不同部门,现有4名在校大学生来该公司实习,要求安排到该公司的两个部门,且每部门安排两名,则不同的安排方案种数为( )
| A. | 40 | B. | 60 | C. | 120 | D. | 240 |
16.若sin(π-α)=$\frac{1}{3}$,且$\frac{π}{2}$≤α≤π,则sin2α的值为( )
| A. | -$\frac{4\sqrt{2}}{9}$ | B. | -$\frac{2\sqrt{2}}{9}$ | C. | $\frac{2\sqrt{2}}{9}$ | D. | $\frac{4\sqrt{2}}{9}$ |

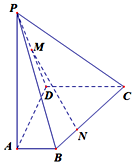 如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是直角梯形,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点M为PD的中点,点N是为棱CB上一点,且$\overrightarrow{BN}=λ\overrightarrow{BC},λ∈({0,1})$.
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是直角梯形,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点M为PD的中点,点N是为棱CB上一点,且$\overrightarrow{BN}=λ\overrightarrow{BC},λ∈({0,1})$.