题目内容
随机调查某校50个学生的午餐费,结果如下表,这50个学生午餐费的平均值和方差分别是( )
| 餐费(元) | 3 | 4 | 5 |
| 人数 | 10 | 20 | 20 |
| A、4,0.6 | ||
B、4,
| ||
| C、4.2,0.56 | ||
D、4.2,
|
考点:极差、方差与标准差
专题:概率与统计
分析:根据题目中的数据,求出它们的平均数和方差即可.
解答:
解:根据题意,得
这50个学生午餐费的平均值是
=
(3×10+4×20+5×20)=4.2,
方差是
s2=
[10×(3-4.2)2+20×(4-4.2)2+20×(5-4.2)2]=0.56.
故选:C.
这50个学生午餐费的平均值是
. |
| x |
| 1 |
| 50 |
方差是
s2=
| 1 |
| 50 |
故选:C.
点评:本题考查了计算加权平均数和方差的问题,解题时应根据平均数与方差的公式,进行计算,即可得出正确的答案,是基础题.

练习册系列答案
相关题目
已知直线2x+3y-3=0和4x+my+2=0互相平行,则两直线之间的距离是( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、4 |
已知集合M={x|
>1},N={y|y=x2+1},则M∩N=( )
| 2 |
| x |
| A、[1,2) | B、(1,2) |
| C、(2,+∞) | D、∅ |
在一个投掷硬币的游戏中,把一枚硬币连续抛两次,记“第一次出现正面”为事件A,“第二次出现正面”为事件B,则P(B|A)等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
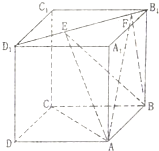 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=
| ||
| 2 |
①AC⊥BE;
②平面AEF与平面ABCD的交线平行于直线EF;
③异面直线AE,BF所成的角为定值;
④三棱锥A-BEF的体积为定值,其中错误结论的个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
直线ax-y+3=0与圆(x-1)2+(y-2)2=4相交于A、B两点,且弦AB的长为2
,则a=( )
| 3 |
| A、-1 | ||
| B、0 | ||
C、
| ||
| D、1 |
从学号为1~60的高一某班60名学生中随机选取5名同学参加数学测试,采用系统抽样的方法,则所选5名学生的学号可能是( )
| A、10,20,30,40,50 |
| B、6,18,30,42,54 |
| C、2,4,6,8,10 |
| D、4,13,22,31,40 |
观察下列各图,并阅读图形下面的文字,像这样,10条直线相交,交点的个数最多是( )


| A、40 | B、45 | C、50 | D、55 |