题目内容
16.已知数列{an}的首项a1=m,其前n项和为Sn,且满足Sn+Sn+1=3n2+2n,若对?n∈N+,an<an+1恒成立,则m的取值范围是(-2,$\frac{5}{3}$).分析 Sn+Sn+1=3n2+2n,n=1时,2a1+a2=5,解得a2.n≥2时,利用递推关系可得:an+1+an=6n-1,于是an+1-an-1=6,因此数列{an}的奇数项与偶数项分别成等差数列,对n分类讨论即可得出
解答 解:∵Sn+Sn+1=3n2+2n,
∴n=1时,2a1+a2=5,解得a2=5-2m.
n≥2时,Sn-1+Sn=3(n-1)2+2(n-1),
∴an+1+an=6n-1,∴an+an-1=6n-7,
∴an+1-an-1=6,
∴数列{an}的奇数项与偶数项分别成等差数列,
a2k=5-2m+6(k-1)=6k-1-2m,
a2k-1=m+6(k-1)=6k+m-6.
∵对?n∈N*,an<an+1恒成立,
∴n=2k-1时,6k+m-6<6k-1-2m,解得m<$\frac{5}{3}$.
n=2k时,6k-1-2m<6(k+1)+m-6,解得:m>-2.
综上可得m的取值范围是:-2<m<$\frac{5}{3}$.
故答案为:(-2,$\frac{5}{3}$).
点评 本题考查了等差数列通项公式及其求和公式、递推关系、分类讨论方法,考查了推理能力与技能数列,主要考查参数的取值范围的求解,根据条件求出与an的有关的关系式是解决本题的关键,属于中档题.

练习册系列答案
相关题目
6.函数y=lg(|x|+1)的图象大致是( )
| A. | 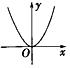 | B. | 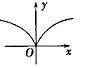 | C. | 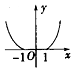 | D. | 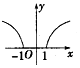 |
11.给出定义:设f′(x)是函数y=f(x)的导函数,f″(x)是函数f′(x)的导函数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.已知函数f(x)=-4x+3sinx-cosx的拐点是M(x0,f(x0)),则点M( )
| A. | 在直线y=-3x上 | B. | 在直线y=3x上 | C. | 在直线y=-4x上 | D. | 在直线y=4x上 |
8.与x轴相切且和半圆x2+y2=4(0≤y≤2)内切的动圆圆心的轨迹方程是( )
| A. | x2=-4(y-1)(0<y≤1) | B. | x2=4(y-1)(0<y≤1) | C. | x2=4(y+1)(0<y≤1) | D. | x2=-2(y-1)(0<y≤1) |