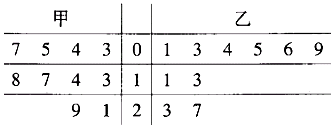
��Ŀ����
7����֪˫����$����{x^2}-\frac{y^2}{b^2}=1$��b��0����ֱ��l��y=kx+m��km��0����l�릣����P��Q���㣬P'ΪP����y��ĶԳƵ㣬ֱ��P'Q��y�ύ�ڵ�N��0��n������1�����㣨2��0���Ǧ���һ�����㣬�Ľ����߷��̣�
��2����b=1����P������Ϊ��-1��0������$\overrightarrow{NP'}=\frac{3}{2}\overrightarrow{P'Q}$����k��ֵ��
��3����m=2����n����b�ı���ʽ��
���� ��1����˫����$����{x^2}-\frac{y^2}{b^2}=1$��b��0�����㣨2��0���Ǧ���һ�����㣬���c=2��a=1���ɴ���������ı����̣��Ӷ���������Ľ����߷��̣�
��2��˫���ߦ�Ϊ��x2-y2=1���ɶ��ȷֵ����깫ʽ�������֪���������k��ֵ��
��3����P��x1��y1����Q��x2��y2����kPQ=k0����${P}^{'}��-{{x}_{1}��{y}_{1}����{l}_{PQ}={k}_{0}x+n}^{\;}$����$\left\{\begin{array}{l}{y=kx+2}\\{{x}^{2}-\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$���ã�b2-k2��x2-4kx-4-b2=0����$\left\{\begin{array}{l}{y={k}_{0}x+n}\\{{x}^{2}-\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$���ã�${b}^{2}-{{k}_{0}}^{2}$��x2-2k0nx-n2-b2=0���ɴ�����Τ�ﶨ���������֪���������n����b�ı���ʽ��
��� �⣺��1����˫����$����{x^2}-\frac{y^2}{b^2}=1$��b��0�����㣨2��0���Ǧ���һ�����㣬
��c=2��a=1����b2=c2-a2=4-1=3��
�ণ�ı�����Ϊ��${x}^{2}-\frac{{y}^{2}}{3}$=1��
���Ľ����߷���Ϊ$y=��\sqrt{3}x$��
��2����b=1����˫���ߦ�Ϊ��x2-y2=1��P��-1��0����P�䣨1��0����
��$\overrightarrow{N{P}^{'}}$=$\frac{3}{2}$$\overrightarrow{{P}^{'}Q}$����Q��x2��y2����
���ж��ȷֵ����깫ʽ���ã�
$\left\{\begin{array}{l}{1=\frac{0+\frac{3}{2}{x}_{2}}{1+\frac{3}{2}}}\\{0=\frac{n+\frac{3}{2}{y}_{2}}{1+\frac{3}{2}}}\end{array}\right.$�����${x}_{2}=\frac{5}{3}$����${{x}_{2}}^{2}-{{y}_{2}}^{2}=1$����${y}_{2}=��\frac{4}{3}$��
��$k=\frac{{y}_{2}-0}{{x}_{2}+1}$=$��\frac{1}{2}$��
��3����P��x1��y1����Q��x2��y2����kPQ=k0��
��${P}^{'}��-{{x}_{1}��{y}_{1}����{l}_{PQ}={k}_{0}x+n}^{\;}$��
��$\left\{\begin{array}{l}{y=kx+2}\\{{x}^{2}-\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$���ã�b2-k2��x2-4kx-4-b2=0��
${x}_{1}+{x}_{2}=\frac{4k}{{b}^{2}-{k}^{2}}$��${x}_{1}{x}_{2}=\frac{-4-{b}^{2}}{{b}^{2}-{k}^{2}}$��
��$\left\{\begin{array}{l}{y={k}_{0}x+n}\\{{x}^{2}-\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$���ã�${b}^{2}-{{k}_{0}}^{2}$��x2-2k0nx-n2-b2=0��
-x1+x2=$\frac{2{k}_{0}n}{{b}^{2}-{{k}_{0}}^{2}}$��-x1x2=$\frac{-{n}^{2}-{b}^{2}}{{b}^{2}-{{k}_{0}}^{2}}$��
��x1x2=$\frac{-4-{b}^{2}}{{b}^{2}-{k}^{2}}$=$\frac{{n}^{2}+{b}^{2}}{{b}^{2}-{{k}_{0}}^{2}}$����$\frac{{b}^{2}-{{k}_{0}}^{2}}{{b}^{2}-{k}^{2}}$����$\frac{{b}^{2}-{{k}_{0}}^{2}}{{b}^{2}-{k}^{2}}$=$\frac{{n}^{2}+{b}^{2}}{-4-{b}^{2}}$��
$\frac{k}{{k}_{0}}$=$\frac{\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}}{\frac{{y}_{2}-{y}_{1}}{{x}_{2}+{x}_{1}}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{2}-{x}_{1}}$=$\frac{2k}{{k}_{0}n}•\frac{{b}^{2}-{{k}_{0}}^{2}}{{b}^{2}-{k}^{2}}$=$\frac{2k}{{k}_{0}n}•\frac{{n}^{2}+{b}^{2}}{-4-{b}^{2}}$��
����2n2+n��4+b2��+2b2=0��
��n=-2��n=$\frac{{b}^{2}}{-2}$��
��n=-2����$\frac{{b}^{2}-{{k}_{0}}^{2}}{{b}^{2}-{k}^{2}}$=$\frac{{n}^{2}+{b}^{2}}{-4-{b}^{2}}$����2b2=k2+k02��
��$\left\{\begin{array}{l}{y={k}_{0}x-2}\\{y=kx+2}\end{array}\right.$����$\left\{\begin{array}{l}{x=\frac{4}{{k}_{0}-k}}\\{y=\frac{2k+2{k}_{0}}{{k}_{0}-k}}\end{array}\right.$��
��Q��$\frac{4}{{k}_{0}-k}$��$\frac{2k+2{k}_{0}}{{k}_{0}-k}$��������x2-$\frac{{y}^{2}}{{b}^{2}}$=1�����ã�
${b}^{2}-��4+k{k}_{0}��{b}^{2}+4k{k}_{0}=0$�����b2=4��b2=kk0��
��b2=4ʱ������n=$\frac{{b}^{2}}{-2}$��
��b2=kk0ʱ����2b2=k2+k02����k=k0����ȥ����
���ϣ���n=$\frac{{b}^{2}}{-2}$��
���� ���⿼��˫���ߵĽ����ߵ�������ֱ�ߵ�б�ʵ�������n����b�ı���ʽ�������е��⣬����ʱҪ�������⣬ע��˫���ߡ�ֱ�ߡ�Τ�ﶨ���ĺ������ã�

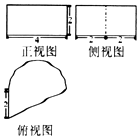 ��֪һ�����������ͼ��ͼ��ʾ������ͼ��һ��ֱ����������һ����Բ��ɣ���ü���������Ϊ��������
��֪һ�����������ͼ��ͼ��ʾ������ͼ��һ��ֱ����������һ����Բ��ɣ���ü���������Ϊ��������| A�� | 4��+8 | B�� | 4��+12 | C�� | 8��+8 | D�� | 8��+12 |
| A�� | $��{1��\frac{{\sqrt{5}}}{2}}��$ | B�� | $��{\sqrt{5}��+��}��$ | C�� | $��{\frac{{\sqrt{5}}}{2}��\sqrt{5}}��$ | D�� | $��{1��\frac{{\sqrt{5}}}{2}}���ȣ�{\sqrt{5}��+��}��$ |
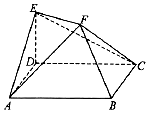 ��ͼ��ABCD�DZ߳�2�����Σ����С�DAB=60�㣬ED��ֱƽ��ABCD��ED=1��EF��BD��2EF=BD��
��ͼ��ABCD�DZ߳�2�����Σ����С�DAB=60�㣬ED��ֱƽ��ABCD��ED=1��EF��BD��2EF=BD��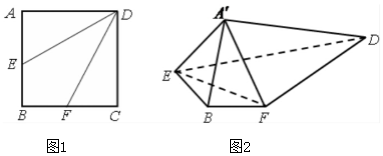 ��ͼ���߳�Ϊ2��������ABCD�У���E��AB���е㣬��F��BC���е㣮����AED����DCF�ֱ���DE��DF����ʹA��C�����غ��ڵ�A'������EF��A'B��
��ͼ���߳�Ϊ2��������ABCD�У���E��AB���е㣬��F��BC���е㣮����AED����DCF�ֱ���DE��DF����ʹA��C�����غ��ڵ�A'������EF��A'B��