题目内容
8.与x轴相切且和半圆x2+y2=4(0≤y≤2)内切的动圆圆心的轨迹方程是( )| A. | x2=-4(y-1)(0<y≤1) | B. | x2=4(y-1)(0<y≤1) | C. | x2=4(y+1)(0<y≤1) | D. | x2=-2(y-1)(0<y≤1) |
分析 当两圆内切时,根据两圆心之间的距离等于两半径相减可得动圆圆心的轨迹方程.
解答 解:设动圆圆心为M(x,y),做MN⊥x轴交x轴于N.
因为两圆内切,|MO|=2-|MN|,
所以$\sqrt{{x}^{2}+{y}^{2}}$=2-y,
化简得x2=4-4y(1≥y>0)
故选A.
点评 此题考查学生掌握圆与圆的位置关系所满足的条件,考学生的计算能力,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下列四个命题中,真命题的是( )
| A. | 空间中两组对边分别相等的四边形为平行四边形 | |
| B. | 所有梯形都有外接圆 | |
| C. | 所有的质数的平方都不是偶数 | |
| D. | 不存在一个奇数,它的立方是偶数 |
20.从点A(2,-1,7)沿向量$\overrightarrow{a}$=(8,9,-12)的方向取线段长|AB|=34,则B点的坐标为( )
| A. | (18,17,-17) | B. | (-14,-19,17) | C. | $({6,\frac{7}{2},1})$ | D. | $({-2,-\frac{11}{2},13})$ |
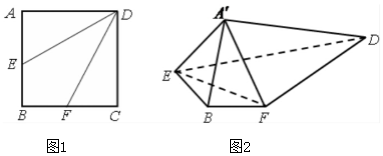 如图,边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点.将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A',连结EF,A'B.
如图,边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点.将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A',连结EF,A'B. 如图,圆(x+2)2+y2=4的圆心为点B,A(2,0),P是圆上任意一点,线段AP的垂直平分线l和直线BP相交于点Q,当点P在圆上运动时,点Q的轨迹方程为${x^2}-\frac{y^2}{3}=1$.
如图,圆(x+2)2+y2=4的圆心为点B,A(2,0),P是圆上任意一点,线段AP的垂直平分线l和直线BP相交于点Q,当点P在圆上运动时,点Q的轨迹方程为${x^2}-\frac{y^2}{3}=1$.
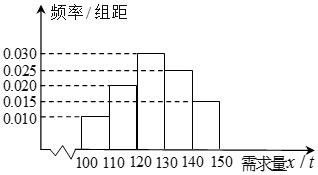 随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.