题目内容
11.给出定义:设f′(x)是函数y=f(x)的导函数,f″(x)是函数f′(x)的导函数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.已知函数f(x)=-4x+3sinx-cosx的拐点是M(x0,f(x0)),则点M( )| A. | 在直线y=-3x上 | B. | 在直线y=3x上 | C. | 在直线y=-4x上 | D. | 在直线y=4x上 |
分析 根据拐点的定义,结合导数公式求出M的坐标,利用直线的斜率公式进行求解即可.
解答 解:函数的导数f′(x)=-4+3cosx+sinx,
f''(x)=-3sinx+cosx,
由f''(x)=-3sinx+cosx=0得3sinx=cosx,即tanx=$\frac{1}{3}$,
不妨取x=arctan$\frac{1}{3}$,
则f(arctan$\frac{1}{3}$)=-4×arctan$\frac{1}{3}$,
M(x0,f(x0))在直线y=-4x上,
故选:C
点评 本题主要考查函数的导数的计算,根据拐点的定义求出M的坐标是解决本题的关键.

练习册系列答案
相关题目
2.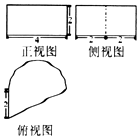 已知一几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的体积为( )
已知一几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的体积为( )
 已知一几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的体积为( )
已知一几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的体积为( )| A. | 4π+8 | B. | 4π+12 | C. | 8π+8 | D. | 8π+12 |
3.下列四个命题中,真命题的是( )
| A. | 空间中两组对边分别相等的四边形为平行四边形 | |
| B. | 所有梯形都有外接圆 | |
| C. | 所有的质数的平方都不是偶数 | |
| D. | 不存在一个奇数,它的立方是偶数 |
20.从点A(2,-1,7)沿向量$\overrightarrow{a}$=(8,9,-12)的方向取线段长|AB|=34,则B点的坐标为( )
| A. | (18,17,-17) | B. | (-14,-19,17) | C. | $({6,\frac{7}{2},1})$ | D. | $({-2,-\frac{11}{2},13})$ |
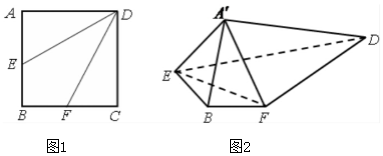 如图,边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点.将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A',连结EF,A'B.
如图,边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点.将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A',连结EF,A'B.