题目内容
四棱锥的底面是正方形,侧棱与底面所成的角都等于60°,它的所有顶点都在直径为2的球面上,则该四棱锥的体积等于 .
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:设正方形ABCD的边长为a,由题意得BD=AC=PA=PB=PC=PD=
a,设O为球心,由题意知OP=OB=1,BE=
a,PE=
a,由勾股定理求出a=
,由此能求出该四棱锥的体积.
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
解答:
解:如图,四棱锥P-ABCD的底面ABCD是正方形,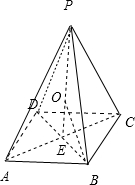
侧棱与底面所成的角都等于60°,
设正方形ABCD的边长为a,
则BD=AC=PA=PB=PC=PD=
a,
设O为球心,由题意知OP=OB=1,BE=
a,
PE=
=
a,
∴(
a)2+(
a-1)2=1,解得a=
,
∴PE=
×
=
,
∴该四棱锥的体积V=
×S正方形ABCD×PE=
×(
)2×
=
.
故答案为:
.

侧棱与底面所成的角都等于60°,
设正方形ABCD的边长为a,
则BD=AC=PA=PB=PC=PD=
| 2 |
设O为球心,由题意知OP=OB=1,BE=
| ||
| 2 |
PE=
2a2-(
|
| ||
| 2 |
∴(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴PE=
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
∴该四棱锥的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题考查四棱锥的体积的求法,解题时要认真审题,注意空间思维能力的培养,是中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目