题目内容
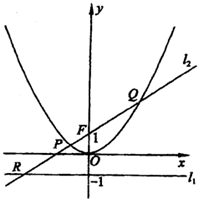
已知定点F(0,1)和直线l1:y=-1,过定点F与直线l1相切的动圆的圆心为点C.
(Ⅰ)求动点C的轨迹方程;
(Ⅱ)过点F的直线l2交轨迹于两点P、Q,交直线l1于点R,求
•
最小值,并求此时的直线l2的方程.
(Ⅰ)求动点C的轨迹方程;
(Ⅱ)过点F的直线l2交轨迹于两点P、Q,交直线l1于点R,求
| RP |
| RQ |
考点:轨迹方程,平面向量数量积的运算
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)根据点G到点F的距离等于它到l1的距离,依据抛物线的定义可知点G的轨迹是以F为焦点,l1为准线的抛物线,进而求得其轨迹方程.
(2)设出直线l2的方程与抛物线方程联立消去y,设出P,Q的坐标,根据韦达定理表示出x1+x2和x1x2的表达式,进而可得点R的坐标,表示出
•
,根据均值不等式求得其最小值.
(2)设出直线l2的方程与抛物线方程联立消去y,设出P,Q的坐标,根据韦达定理表示出x1+x2和x1x2的表达式,进而可得点R的坐标,表示出
| RP |
| RQ |
解答:
 解:(1)由题设点G到点F的距离等于它到l1的距离,
解:(1)由题设点G到点F的距离等于它到l1的距离,
∴点G的轨迹是以F为焦点,l1为准线的抛物线,
∴所求轨迹的方程为x2=4y;
(2)由题意直线l2的方程为y=kx+1,
与抛物线方程联立消去y得x2-4kx-4=0.
记P(x1,y1),Q(x2,y2),
则x1+x2=4k,x1x2=-4.
∵直线PQ的斜率k≠0,易得点R的坐标为(-
,-1),
∴
•
=(1+k2)x1x2+(
+2k)(x1+x2)+
+4=4(k2+
)+8≥16,当且仅当k2=1时取到等号,
∴
•
的最小值为16.此时直线l2的方程为x+y-1=0或x-y+1=0.
 解:(1)由题设点G到点F的距离等于它到l1的距离,
解:(1)由题设点G到点F的距离等于它到l1的距离,∴点G的轨迹是以F为焦点,l1为准线的抛物线,
∴所求轨迹的方程为x2=4y;
(2)由题意直线l2的方程为y=kx+1,
与抛物线方程联立消去y得x2-4kx-4=0.
记P(x1,y1),Q(x2,y2),
则x1+x2=4k,x1x2=-4.
∵直线PQ的斜率k≠0,易得点R的坐标为(-
| 2 |
| k |
∴
| RP |
| RQ |
| 2 |
| k |
| 4 |
| k2 |
| 1 |
| k2 |
∴
| RP |
| RQ |
点评:本题考查抛物线方程,考查了直线与圆锥曲线的关系,考查基本不等式的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD的边BC垂直于圆O所在的平面,且AB=2,AD=EF=1.
如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD的边BC垂直于圆O所在的平面,且AB=2,AD=EF=1. 某校高一年级共有四个班,在一次数学调研测试后,随机地在各班抽取部分学生进行成绩分析.各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的成绩统计结果的频率分直方图如图所示,其中120~130(包括120分但不包括130分)分数段的人数为5人.
某校高一年级共有四个班,在一次数学调研测试后,随机地在各班抽取部分学生进行成绩分析.各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的成绩统计结果的频率分直方图如图所示,其中120~130(包括120分但不包括130分)分数段的人数为5人.