题目内容
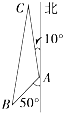我舰在敌岛A处南偏西50°的B处，且AB距离为12海里，发现敌舰正离开岛沿北偏西10°的方向以每小时10海里的速度航行，若我舰要用2小时追上敌舰，则速度大小为（ ）| A、28海里/小时 | ||
| B、14海里/小时 | ||
C、14
| ||
| D、20海里/小时 |
考点：解三角形的实际应用
专题：应用题,解三角形
分析：由题意推出∠BAC=120°，利用余弦定理求出BC=28，然后推出渔船甲的速度．
解答：
解：依题意，∠BAC=120°，AB=12，AC=10×2=20，
在△ABC中，由余弦定理，
得BC2=AB2+AC2-2AB×AC×cos∠BAC=122+202-2×12×20×cos120°=784．
解得BC=28．所以渔船甲的速度为
=14海里/小时．
故我舰要用2小时追上敌舰速度大小为：14海里/小时．
故选：B．
在△ABC中，由余弦定理，
得BC2=AB2+AC2-2AB×AC×cos∠BAC=122+202-2×12×20×cos120°=784．
解得BC=28．所以渔船甲的速度为
| BC |
| 2 |
故我舰要用2小时追上敌舰速度大小为：14海里/小时．
故选：B．
点评：本题是中档题，考查三角函数在实际问题中的应用，余弦定理的应用，考查计算能力．
练习册系列答案
阅读快车系列答案
相关题目
不等式|x2-1|＞3的解集为（ ）
| A、（-2，2） |
| B、（-∞，-1）∪（1，+∞） |
| C、（-1，1） |
| D、（-∞，-2）∪（2，+∞） |
设以
=（1，-2）为方向向量的直线的倾斜角为α，则sin（2α+
）=（ ）
. |
| e |
| π |
| 4 |
A、
| ||||
B、7
| ||||
C、
| ||||
D、-
|
用一个平面去截正方体，则截面不可能是（ ）
| A、正三角形 | B、正方形 |
| C、正五边形 | D、正六边形 |
已知函数f（x）=
若|f（x）|≥a（x-1），则a的取值范围是（ ）
|
| A、（-∞，-1） |
| B、[-1，1] |
| C、[0，1] |
| D、[-1，0] |
已知函数f（x）=ln（1+x）-
，若x≥0时，f（x）≤0，则λ的最小值为（ ）
| x(1+λx) |
| 1+x |
| A、0 | ||
B、
| ||
| C、1 | ||
| D、2 |
设F1，F2是双曲线
-
=1的焦点，P是双曲线上一点．若P到F1的距离为9，则P到F2的距离等于（ ）
| x2 |
| 16 |
| y2 |
| 20 |
| A、0 | ||
| B、17 | ||
C、
| ||
| D、2 |