题目内容
17.设A,B为相互独立事件,下列命题中正确的是( )| A. | A与B是对立事件 | B. | A与B是互斥事件 | ||
| C. | A与$\overline{B}$是相互独立事件 | D. | $\overline{A}$与$\overline{B}$不相互独立 |
分析 相互独立事件是一个事件对另一个事件发生的概率没有影响;互斥事件是一个事件发生,另一个事件就不发生,互斥事件不一定是对立事件,对立事件一定是互斥事件;由相互独立事件以及互斥、对立事件的概念判定选项中的正确命题.
解答 解:A中,A与B是相互独立事件,但A与B不一定是对立事件,∴A错误;
B中,A与B是相互独立事件,但是A与B不一定是互斥事件,∴B错误;
C中,当A与B是相互独立事件时,A与$\overline{B}$是相互独立事件,∴C正确;
D中,A与B是相互独立事件时,$\overline{A}$与$\overline{B}$不是相互独立事件,是错误的;
故选:C
点评 本题考查了相互独立事件与互斥、对立事件之间的判定问题,是基础题.

练习册系列答案
相关题目
7.要得到函数$y=cos(\frac{x}{2}-\frac{π}{3})$的图象,只需将函数$y=cos\frac{x}{2}$的图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{2π}{3}$个单位 | D. | 向右平移$\frac{2π}{3}$个单位 |
8.函数y=cosx图象上任意一点处的切线倾斜角为α,则α取值范围为( )
| A. | (0,π) | B. | [0,$\frac{π}{4}$] | C. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π) | D. | [0,$\frac{π}{4}$]∪($\frac{π}{2}$,$\frac{3π}{4}$] |
12.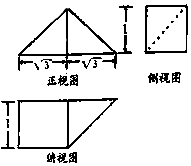 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的体积( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的体积( )
 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的体积( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的体积( )| A. | $\frac{{5\sqrt{3}}}{6}$ | B. | $\frac{{7\sqrt{3}}}{6}$ | C. | $\frac{{\sqrt{3}}}{6}$ | D. | $\frac{{3\sqrt{3}}}{6}$ |
2.给出如下“三段论”的推理过程:
因为对数函数y=logax(a>0且a≠1)是增函数,…大前提
而y=${log}_{\frac{1}{2}}x$是对数函数,…小前提
所以y=${log}_{\frac{1}{2}}x$是增函数,…结论
则下列说法正确的是( )
因为对数函数y=logax(a>0且a≠1)是增函数,…大前提
而y=${log}_{\frac{1}{2}}x$是对数函数,…小前提
所以y=${log}_{\frac{1}{2}}x$是增函数,…结论
则下列说法正确的是( )
| A. | 推理形式错误 | B. | 大前提错误 | ||
| C. | 小前提错误 | D. | 大前提和小前提都错误 |
7.已知a为函数f(x)=x3-3x的极小值点,则a=( )
| A. | -1 | B. | -2 | C. | 2 | D. | 1 |
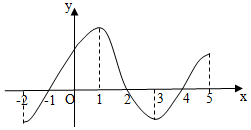 如图是函数y=f(x)的导数的图象,则正确的判断是(2)(4).
如图是函数y=f(x)的导数的图象,则正确的判断是(2)(4).



