题目内容
12.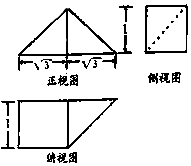 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的体积( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的体积( )| A. | $\frac{{5\sqrt{3}}}{6}$ | B. | $\frac{{7\sqrt{3}}}{6}$ | C. | $\frac{{\sqrt{3}}}{6}$ | D. | $\frac{{3\sqrt{3}}}{6}$ |
分析 由已知中的三视图,可知该几何体左边是四棱锥,即“阳马”,右边是直三棱柱,即“堑堵”,该几何体的体积只需把“阳马”,和“堑堵”体积分别计算相加即可.
解答 解:由三视图知:几何体左边是四棱锥,即“阳马”,底面边长为1和$\sqrt{3}$,高为1,其体积V1=$\frac{1}{3}$×$\sqrt{3}$×1=$\frac{\sqrt{3}}{3}$
右边是直三棱柱,即“堑堵”,底面边长是$\sqrt{3}$和1的直角三角形,高为1,其体积V2=$\frac{1}{2}×1×\sqrt{3}=\frac{\sqrt{3}}{2}$
∴该几何体的体积V=${V}_{1}+{V}_{2}=\frac{\sqrt{3}}{3}+\frac{\sqrt{3}}{2}=\frac{5\sqrt{3}}{6}$.
故选:A.
点评 本题考查了四棱锥与三棱柱的三视图及其体积计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
7.为了加强某站的安全检查,从甲乙丙等5名候选民警中选2名作为安保人员,则甲乙丙中有2人被选中的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{1}{10}$ | C. | $\frac{3}{20}$ | D. | $\frac{1}{20}$ |
17.设A,B为相互独立事件,下列命题中正确的是( )
| A. | A与B是对立事件 | B. | A与B是互斥事件 | ||
| C. | A与$\overline{B}$是相互独立事件 | D. | $\overline{A}$与$\overline{B}$不相互独立 |
4.在区间(0,+∞)内,函数f(x)=ex-x是( )
| A. | 增函数 | B. | 减函数 | C. | 先增后减 | D. | 先减后增 |
1.已知向量$\vec a=(2,-3,1),\vec b=(-4,2,x)$,且$\vec a⊥\vec b$,则x的值为( )
| A. | 12 | B. | 10 | C. | -14 | D. | 14 |
2.等差数列的前4项之和为30,前8项之和为100,则它的前12项之和为( )
| A. | 130 | B. | 170 | C. | 210 | D. | 260 |