题目内容
9.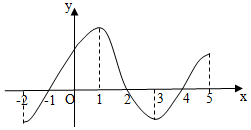 如图是函数y=f(x)的导数的图象,则正确的判断是(2)(4).
如图是函数y=f(x)的导数的图象,则正确的判断是(2)(4).(1)f(x)在(-2,1)上是增函数;
(2)x=-1是f(x)的极小值点;
(3)x=2是f(x)的极小值点;
(4)f(x)在(2,4)上是减函数,在(-1,2)上是增函数.
分析 由导数的符号为正,原函数为增函数;导数的符号为负,原函数为减函数,即可判断(1)错,(4)正确;
由某点处的导数左正右负,即为极大值点,左负右正,即为极小值点,即可判断(2)正确,(3)错.
解答 解:对于(1)由导数的图象可得f(x)在(-2,-1)导数为负的,即f(x)递减;在(-1,1)导数大于0,即
f(x)递增.故(1)不正确;
对于(2),由图象可得f(x)的导数在x=-1处左负右正,为极小值点,故(2)正确;
对于(3),由图象可得f(x)的导数在x=2处左正右负,为极大值点,故(3)不正确;
对于(4),由导数的图象可得,f(x)在(2,4)上导数小于0,即f(x)是减函数,
在(-1,2)上导数大于0,即f(x)是增函数.故(4)正确.
故答案为:(2),(4).
点评 本题考查命题的真假判断和应用,主要是导数的运用:求极值和单调区间,注意运用数形结合思想方法,属于基础题.

练习册系列答案
相关题目
19. 将正方体切去一个三棱锥得到几何体的三视图如图所示,则该几何体的体积为( )
将正方体切去一个三棱锥得到几何体的三视图如图所示,则该几何体的体积为( )
 将正方体切去一个三棱锥得到几何体的三视图如图所示,则该几何体的体积为( )
将正方体切去一个三棱锥得到几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{22}{3}$ | B. | $\frac{20}{3}$ | C. | $\frac{16}{3}$ | D. | 6 |
17.设A,B为相互独立事件,下列命题中正确的是( )
| A. | A与B是对立事件 | B. | A与B是互斥事件 | ||
| C. | A与$\overline{B}$是相互独立事件 | D. | $\overline{A}$与$\overline{B}$不相互独立 |
4.在区间(0,+∞)内,函数f(x)=ex-x是( )
| A. | 增函数 | B. | 减函数 | C. | 先增后减 | D. | 先减后增 |
1.已知向量$\vec a=(2,-3,1),\vec b=(-4,2,x)$,且$\vec a⊥\vec b$,则x的值为( )
| A. | 12 | B. | 10 | C. | -14 | D. | 14 |