题目内容
4.已知集合A={x|lnx≤0},B={x∈R|z=x+i,$|z|≥\frac{{\sqrt{5}}}{2}$,i是虚数单位},A∩B=( )| A. | $({-∞,-\frac{1}{2}}]∪[{\frac{1}{2},1}]$ | B. | $[{\frac{1}{2},1}]$ | C. | (0,1] | D. | [1,+∞) |
分析 先分别求出集合A和B,由此利用交集定义能求出A∩B.
解答 解:∵集合A={x|lnx≤0}={x|0<x≤1},
B={x∈R|z=x+i,$|z|≥\frac{{\sqrt{5}}}{2}$,i是虚数单位}={x|x≥$\frac{1}{2}$或x$≤-\frac{1}{2}$},
∴A∩B={x|$\frac{1}{2}≤x≤1$}=[$\frac{1}{2},1$].
故选:B.
点评 本题考查交集的求法,是基础题,解题时要认真审题,注意交集定义的合理运用.

练习册系列答案
相关题目
14.已知i为虚数单位,$\overline z$是复数z的共轭复数,若$z=cos\frac{2π}{3}+isin\frac{2π}{3}$,则$\overline z$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.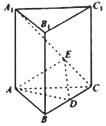 在底面为正三角形的直棱柱(侧棱垂直于底面的棱柱)ABC-A1B1C1中,AB=2,AA1=3,点D为棱BD的中点,点E为A,C上的点,且满足A1E=mEC(m∈R),当二面角E-AD-C的余弦值为$\frac{\sqrt{10}}{10}$时,实数m的值为( )
在底面为正三角形的直棱柱(侧棱垂直于底面的棱柱)ABC-A1B1C1中,AB=2,AA1=3,点D为棱BD的中点,点E为A,C上的点,且满足A1E=mEC(m∈R),当二面角E-AD-C的余弦值为$\frac{\sqrt{10}}{10}$时,实数m的值为( )
 在底面为正三角形的直棱柱(侧棱垂直于底面的棱柱)ABC-A1B1C1中,AB=2,AA1=3,点D为棱BD的中点,点E为A,C上的点,且满足A1E=mEC(m∈R),当二面角E-AD-C的余弦值为$\frac{\sqrt{10}}{10}$时,实数m的值为( )
在底面为正三角形的直棱柱(侧棱垂直于底面的棱柱)ABC-A1B1C1中,AB=2,AA1=3,点D为棱BD的中点,点E为A,C上的点,且满足A1E=mEC(m∈R),当二面角E-AD-C的余弦值为$\frac{\sqrt{10}}{10}$时,实数m的值为( )| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | 3 |
12.某公共汽车上有10位乘客,沿途5个车站,乘客下车的可能方式有( )种.
| A. | 510 | B. | 105 | C. | 50 | D. | A105 |
19.对于下列表格所示的五个散点,已知求得的线性回归直线方程为$\stackrel{∧}{y}$=0.8x-155.
则实数m的值为12.
| x | 197 | 198 | 201 | 204 | 205 |
| y | 1 | 3 | 6 | 7 | m |
16.若点P对应的复数z满足|z|≤1,则P的轨迹是( )
| A. | 直线 | B. | 线段 | C. | 圆 | D. | 单位圆以及圆内 |
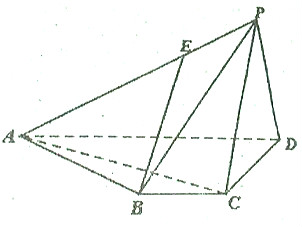 如图,四棱锥P-ABCD中,BC∥AD,BC=1,AD=3,AC⊥CD,且平面PCD⊥平面ABCD.
如图,四棱锥P-ABCD中,BC∥AD,BC=1,AD=3,AC⊥CD,且平面PCD⊥平面ABCD.