题目内容
15.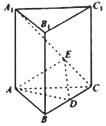 在底面为正三角形的直棱柱(侧棱垂直于底面的棱柱)ABC-A1B1C1中,AB=2,AA1=3,点D为棱BD的中点,点E为A,C上的点,且满足A1E=mEC(m∈R),当二面角E-AD-C的余弦值为$\frac{\sqrt{10}}{10}$时,实数m的值为( )
在底面为正三角形的直棱柱(侧棱垂直于底面的棱柱)ABC-A1B1C1中,AB=2,AA1=3,点D为棱BD的中点,点E为A,C上的点,且满足A1E=mEC(m∈R),当二面角E-AD-C的余弦值为$\frac{\sqrt{10}}{10}$时,实数m的值为( )| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | 3 |
分析 由题意画出图形,在正三棱柱ABC-A1B1C1中,取AC中点O,以O为坐标原点,以OB、OC所在直线为x、y轴建立如图所示空间直角坐标系,求出平面AED的一个法向量(用含有m的代数式表示),再求得平面ADC的一个法向量,结合二面角E-AD-C的余弦值为$\frac{\sqrt{10}}{10}$列式求得m值.
解答 解:在正三棱柱ABC-A1B1C1中,取AC中点O,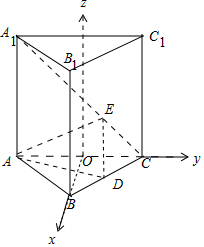
以O为坐标原点,以OB、OC所在直线为x、y轴建立如图所示空间直角坐标系,
∵AB=2,AA1=3,点D为棱BD的中点,
∴A(0,-1,0),C(0,1,0),D($\frac{\sqrt{3}}{2},\frac{1}{2},0$),
A1(0,-1,3),
又点E为A1C上的点,且满足A1E=mEC(m∈R),
∴$\overrightarrow{{A}_{1}E}=m\overrightarrow{EC}$,
设E(x,y,z),则$\overrightarrow{{A}_{1}E}=(x,y+1,z-3)$,$\overrightarrow{EC}=(-x,1-y,-z)$,
∴(x,y+1,z-3)=(-mx,m-my,-mz),得x=0,y=$\frac{m-1}{m+1}$,
z=$\frac{3}{m+1}$.
∴E(0,$\frac{m-1}{m+1}$,$\frac{3}{m+1}$),
则$\overrightarrow{AD}=(\frac{\sqrt{3}}{2},\frac{3}{2},0)$,$\overrightarrow{AE}=(0,\frac{2m}{m+1},\frac{3}{m+1})$,
设平面AED的一个法向量为$\overrightarrow{m}=(x,y,z)$,
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AD}=\frac{\sqrt{3}}{2}x+\frac{3}{2}y=0}\\{\overrightarrow{m}•\overrightarrow{AE}=\frac{2m}{m+1}y+\frac{3}{m+1}z=0}\end{array}\right.$,取x=$-\sqrt{3}$,得$\overrightarrow{m}=(-\sqrt{3},1,-\frac{2}{3}m)$.
平面ADC的一个法向量$\overrightarrow{n}=(0,0,1)$.
∴|cos<$\overrightarrow{m},\overrightarrow{n}$>|=|$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$|=|$\frac{\frac{2}{3}m}{\sqrt{3+1+\frac{4}{9}{m}^{2}}×1}$|=$\frac{\sqrt{10}}{10}$.
解得:m=1.
故选:A.
点评 本题考查二面角的平面角及其求法,训练了利用空间向量求解二面角的大小,是中档题.

| A. | ?α∈R,使得sin2α+cos2α=1 | B. | ?α∈R,使得sin2α+cos2α≠1 | ||
| C. | ?α∈R,使得sin2α+cos2α=1 | D. | ?α∈R,使得sin2α+cos2α≠1 |
| A. | 1 | B. | $\frac{1}{2}$ | C. | -1 | D. | $-\frac{1}{2}$ |
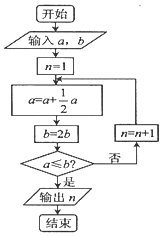 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为3,2,则输出的n=( )
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为3,2,则输出的n=( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | $({-∞,-\frac{1}{2}}]∪[{\frac{1}{2},1}]$ | B. | $[{\frac{1}{2},1}]$ | C. | (0,1] | D. | [1,+∞) |
| A. | [-$\frac{1}{2}$,+∞) | B. | [-$\frac{3}{2}$,+∞) | C. | [-1,+∞) | D. | [-2,+∞) |