题目内容
10.在△ABC中,角A、B、C的对边分别为a、b、c,A=2B.(I )若sinB=$\frac{\sqrt{5}}{5}$,求cosC的值;
(II)若C为钝角,求$\frac{c}{b}$的取值范围.
分析 (Ⅰ)由已知利用同角三角函数基本关系式可求cosB的值,利用二倍角公式可求sinA,cosA的值,由三角形内角和定理,两角和的余弦函数公式即可计算得解.
(Ⅱ)由已知及三角形内角和定理可得0<B<$\frac{π}{6}$,由正弦定理,三角函数恒等变换的应用可得$\frac{c}{b}$=4cos2B-1,由余弦函数的图象和性质可求其取值范围.
解答 (本题满分为12分)
解:(Ⅰ)∵B=$\frac{A}{2}$∈(0,$\frac{π}{2}$),
∴cosB=$\sqrt{1-sin2B}$=$\frac{2\sqrt{5}}{5}$,…(1分)
∵A=2B,
∴sinA=2sinBcosB=$\frac{4}{5}$,cosA=cos2B=1-2sin2B=$\frac{3}{5}$,…(3分)
∴cosC=cos[π-(A+B)]=-cos(A+B)=sinAsinB-cosAcosB=-$\frac{2\sqrt{5}}{25}$.…(5分)
(Ⅱ)∵A=2B,
∴C=π-3B,
又$\frac{π}{2}$<C<π,
∴$\frac{π}{2}$<π-3B<π,0<B<$\frac{π}{6}$.…(7分)
由正弦定理,得
$\frac{c}{b}$=$\frac{sinC}{sinB}$=$\frac{sin(π-3B)}{sinB}$=$\frac{sin3B}{sinB}$=$\frac{sin(2B+B)}{sinB}$=$\frac{sin2BcosB+cos2BsinB}{sinB}$
=$\frac{2sinBcos2B+cos2BsinB}{sinB}$=2cos2B+cos2B=4cos2B-1,…(10分)
∵$\frac{\sqrt{3}}{2}$<cosB<1,
∴2<$\frac{c}{b}$<3,
故$\frac{c}{b}$的取值范围是(2,3).…(12分)
点评 本题主要考查了三角函数恒等变换的应用,三角形内角和定理,余弦函数的图象和性质,正弦定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

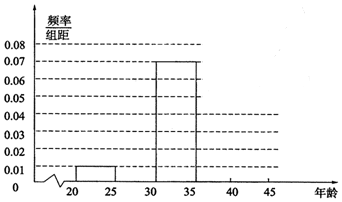
| 分组(单位:岁) | 频数 | 频率 |
| [20,25) | 5 | 0.050 |
| [25,30) | ① | 0.200 |
| [30,35) | 35 | ② |
| [35,40) | 30 | 0.300 |
| [40,45) | 10 | 0.100 |
| 合计 | 100 | 1.00 |
(Ⅱ)在抽出的100名职工中按年龄再采用分层抽样法抽取20人参加社会公益活动,其中选取2名职工担任领队工作,记这2名职工中“年龄低于30岁”的人数为X,求X的分布列及数学期望E(X).
| 套餐费(元) | 免费主叫时长(分钟) | 免费主叫时长收费(元/分钟) | 免费数据流量(MB) | 超出数据流量收费(元/MB) |
| 38 | 50 | 0.25 | 300 | 0.29 |
| 48 | 50 | 0.25 | 500 | 0.29 |
| 58 | 100 | 0.19 | 500 | 0.29 |
| 88 | 220 | 0.19 | 700 | 0.29 |
| A. | 60分钟和300 MB | B. | 70分钟和500 MB | C. | 100分钟和650 MB | D. | 150分钟和550 MB |
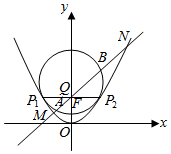 如图,抛物线C:x2=2py(p>0)的准线为y=-1,取过焦点F且平行于x轴的直线与抛物线交于不同的两点P1,P2,过P1,P2作圆心为Q的圆,使抛物线上其余点均在圆外,且∠P1QP2=90°.
如图,抛物线C:x2=2py(p>0)的准线为y=-1,取过焦点F且平行于x轴的直线与抛物线交于不同的两点P1,P2,过P1,P2作圆心为Q的圆,使抛物线上其余点均在圆外,且∠P1QP2=90°.