题目内容
(文)在平面xoy内,不等式x2+y2≤4确定的平面区域为U,不等式组
确定的平面区域为V.
(1)定义横、纵坐标均为非负整数的点为“非负整点”.在区域U中任取2个“非负整点”,求这些“非负整点”中恰好有1个“非负整点”落在区域V中的概率;
(2)在区域U中任取一个点,求这个点恰好在区域V内的概率.
|
(1)定义横、纵坐标均为非负整数的点为“非负整点”.在区域U中任取2个“非负整点”,求这些“非负整点”中恰好有1个“非负整点”落在区域V中的概率;
(2)在区域U中任取一个点,求这个点恰好在区域V内的概率.
考点:几何概型,古典概型及其概率计算公式
专题:计算题,概率与统计
分析:(1)列举法,求出在平面区域V内的非负整点,从(0,0),(0,1),(0,2),(1,0),(2,0),(1,1)中取出2个点的不同情况共有15种,其中恰好有一个在平面区域V内的情况有9种,即可求出概率;
(2)求出扇形区域中心角,可得平面区域V与平面区域U相交部分的面积,求出平面区域U的面积,即可求出结论.
(2)求出扇形区域中心角,可得平面区域V与平面区域U相交部分的面积,求出平面区域U的面积,即可求出结论.
解答:
解:(1)依题可知平面区域U的非负整点为:(0,0),(0,1),(0,2),(1,0),(2,0),(1,1)共有6个,上述非负整点在平面区域V内的为:(0,0),(1,0),(2,0)共有3个,
从(0,0),(0,1),(0,2),(1,0),(2,0),(1,1)中取出2个点的不同情况共有15种,其中恰好有一个在平面区域V内的情况有9种,
∴P1=
=
.
(2)依题可得,平面区域U的面积为4π,设扇形区域中心角为α,则tanα=
=1得α=
,
平面区域V与平面区域U相交部分的面积为
×4π=
.
在区域U任取1个点,则该点在区域V内的概率为P2=
=
.
从(0,0),(0,1),(0,2),(1,0),(2,0),(1,1)中取出2个点的不同情况共有15种,其中恰好有一个在平面区域V内的情况有9种,
∴P1=
| 9 |
| 15 |
| 3 |
| 5 |
(2)依题可得,平面区域U的面积为4π,设扇形区域中心角为α,则tanα=
| ||||
1-
|
| π |
| 4 |
平面区域V与平面区域U相交部分的面积为
| 1 |
| 8 |
| π |
| 2 |
在区域U任取1个点,则该点在区域V内的概率为P2=
| ||
| 4π |
| 1 |
| 8 |
点评:本题考查概率的计算,考查列举法求基本事件,考查几何概型,考查学生的计算能力,确定基本事件的个数是关键.

练习册系列答案
相关题目
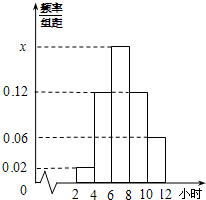 某校为了解学生寒假期间的学习情况,从初中及高中各班共抽取了50名学生,对他们每天平均学习时间进行统计.请根据下面的各班人数统计表和学习时间的频率分布直方图解决下列问题:
某校为了解学生寒假期间的学习情况,从初中及高中各班共抽取了50名学生,对他们每天平均学习时间进行统计.请根据下面的各班人数统计表和学习时间的频率分布直方图解决下列问题: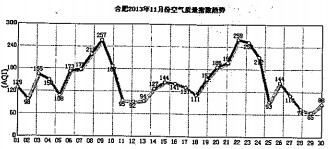 合肥市环保总站对2013年11月合肥市空气质量指数发布如图趋势图.
合肥市环保总站对2013年11月合肥市空气质量指数发布如图趋势图.