题目内容
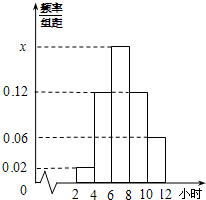 某校为了解学生寒假期间的学习情况,从初中及高中各班共抽取了50名学生,对他们每天平均学习时间进行统计.请根据下面的各班人数统计表和学习时间的频率分布直方图解决下列问题:
某校为了解学生寒假期间的学习情况,从初中及高中各班共抽取了50名学生,对他们每天平均学习时间进行统计.请根据下面的各班人数统计表和学习时间的频率分布直方图解决下列问题:| 年级 | 人数 |
| 初一 | 4 |
| 初二 | 4 |
| 初三 | 6 |
| 高一 | 12 |
| 高二 | 6 |
| 高三 | 18 |
| 合计 | 50 |
(Ⅱ)经调查,每天平均学习时间不少于6小时的学生均来自高中.现采用分层抽样的方法,从学习时间不少于6小时的学生中随机抽取6名学生进行问卷调查,求这三个年级各抽取了多少名学生;
(Ⅲ)在(Ⅱ)抽取的6名学生中随机选取2人进行访谈,求这2名学生来自不同年级的概率.
考点:频率分布直方图,古典概型及其概率计算公式
专题:计算题,概率与统计
分析:(I)利用频率分布直方图中所有小矩形的面积之和为1,求得学习时间为6~8小时的频率,再根据频数=频率×样本容量求解;
(II)求得分层抽样的抽取比例,再根据高中三个年级的人数分别乘以抽取比例可得三个年级的抽取人数;
(III)利用列举法写出从6名学生中选取2人所有可能的情形,从中找出2名学生来自不同年级的情形,利用个数比求概率.
(II)求得分层抽样的抽取比例,再根据高中三个年级的人数分别乘以抽取比例可得三个年级的抽取人数;
(III)利用列举法写出从6名学生中选取2人所有可能的情形,从中找出2名学生来自不同年级的情形,利用个数比求概率.
解答:
解:(Ⅰ)由直方图知,学习时间为6~8小时的频率为1-(0.02+2×0.12+0.06)×2=0.36,
∴学习时间为~小时的人数为50×0.36=18;
(Ⅱ)由直方图可得,学习时间不少于 6小时的学生有18+12+6=36 人.
∵从中抽取6名学生的抽取比例为
=
,高中三个年级的人数分别为12、6、18,
∴从高中三个年级依次抽取2名学生,1名学生,3名学生;
(Ⅲ)设高一的2 名学生为A1,A2高二的 1名学生为B,高三的 3名学生为C1,C2,C3.
则从6名学生中选取2人所有可能的情形有( A1,A2 ),(A1,B ),(A1,C1 ),( A1,C2 ),( A1,C3),(A2,B ),( A2,C1),( A2,C2),(A2,C3 ),(B,C1),(C1,C2 ),(C1,C3 ),(C2,C3),(B,C2),(B,C3 ),共15种可能.
其中2名学生来自不同年级的有( A1,B),(A1,C1 ),( A1,C2 ),(A1,C3),( A2,B),( A2,C1 ),(A2,C2 ),(A2,C3),( B,C1 ),(B,C2 ),( B,C3),共11种情形,
故所求概率为P=
.
∴学习时间为~小时的人数为50×0.36=18;
(Ⅱ)由直方图可得,学习时间不少于 6小时的学生有18+12+6=36 人.
∵从中抽取6名学生的抽取比例为
| 6 |
| 36 |
| 1 |
| 6 |
∴从高中三个年级依次抽取2名学生,1名学生,3名学生;
(Ⅲ)设高一的2 名学生为A1,A2高二的 1名学生为B,高三的 3名学生为C1,C2,C3.
则从6名学生中选取2人所有可能的情形有( A1,A2 ),(A1,B ),(A1,C1 ),( A1,C2 ),( A1,C3),(A2,B ),( A2,C1),( A2,C2),(A2,C3 ),(B,C1),(C1,C2 ),(C1,C3 ),(C2,C3),(B,C2),(B,C3 ),共15种可能.
其中2名学生来自不同年级的有( A1,B),(A1,C1 ),( A1,C2 ),(A1,C3),( A2,B),( A2,C1 ),(A2,C2 ),(A2,C3),( B,C1 ),(B,C2 ),( B,C3),共11种情形,
故所求概率为P=
| 11 |
| 15 |
点评:本题考查了频率分布直方图,古典概型的概率计算,是概率统计的典型题,根据频率分布直方图中频率=
=小矩形的高×组距来获得数据,是解答此类问题的基本方法.
| 频数 |
| 样本容量 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知点P(3,4)和圆C:(x-2)2+y2=4,A,B是圆C上两个动点,且|AB|=2
,则
•(
+
)(O为坐标原点)的取值范围是( )
| 3 |
| OP |
| OA |
| OB |
| A、[3,9] |
| B、[1,11] |
| C、[6,18] |
| D、[2,22] |