题目内容
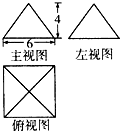
已知某几何体的三视图，则该几何体的体积是（ ）
| A、12 | B、24 | C、36 | D、48 |
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：利用三视图判断几何体的形状，通过三视图是数据，求出几何体的体积即可．
解答：
解：三视图复原的几何体是底面为边长4、3的矩形，高为3的棱锥，高所在棱垂直底面矩形的一个得到，
所以棱锥的体积为：
×4×3×3=12．
故选：A．
解：三视图复原的几何体是底面为边长4、3的矩形，高为3的棱锥，高所在棱垂直底面矩形的一个得到，所以棱锥的体积为：
| 1 |
| 3 |
故选：A．
点评：本题主要考查关于“几何体的三视图”与“几何体的直观图”的相互转化的掌握情况，同时考查空间想象能力．
练习册系列答案
相关题目
如图，四边形ABCD为正方形，△BCE为等腰直角三角形，已知A是△ABC的内角，则“sinA=
”是“tanA=
”的（ ）
| ||
| 2 |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件． |
已知函数f（x）=ax3-bx-3，若f（-1）=7，则f（1）=（ ）
| A、-7 | B、7 | C、-13 | D、13 |
设向量
=（sinα，
）的模为
，则cos2α=（ ）
| a |
| ||
| 2 |
| ||
| 2 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
