题目内容
已知椭圆C的中心在坐标原点,右焦点为F(1,0),A、B是椭圆C的左、右顶点,D是椭圆C上异于A、B的动点,且△ADB面积的最大值为
.
(1)求椭圆C的方程;
(2)是否存在一定点E(x0,0)(0<x0<
),使得当过点E的直线l与曲线C相交于A,B两点时,
+
为定值?若存在,求出定点和定值;若不存在,请说明理由.
| 2 |
(1)求椭圆C的方程;
(2)是否存在一定点E(x0,0)(0<x0<
| 2 |
| 1 | ||
|
|
| 1 | ||
|
|
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设椭圆C的标准方程为
+
=1(a>b>0).由于△ADB面积的最大值为
,可得ab=
.联立
,解得即可得出.
(2)当l与x轴不垂直时,设直线l的参数方程为
(t为参数),代入椭圆方程可得:(1+sin2θ)t2+2tx0cosθ+
-2=0,利用根与系数的关系可得:
+
=
+
=
=
.令4
=-(2
-4),解得
=
.即可得出.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
|
(2)当l与x轴不垂直时,设直线l的参数方程为
|
| x | 2 0 |
| 1 | ||
|
|
| 1 | ||
|
|
| 1 | ||
|
| 1 | ||
|
| (t1+t2)2-2t1t2 |
| (t1t2)2 |
4
| ||||||
(
|
| x | 2 0 |
| x | 2 0 |
| x | 2 0 |
| 2 |
| 3 |
解答:
解:(1)设椭圆C的标准方程为
+
=1(a>b>0).
∵△ADB面积的最大值为
,∴
•2a•b=
,即ab=
.
联立
,解得a=
,b=c=1.
∴椭圆C的方程为
+y2=1.
(2)假设存在一定点 E(x0,0)(0<x0<
),使得当过点 E的直线l与曲线C相交于 A,B两点时,
+
为定值.
当l⊥x轴时,把x0代入椭圆方程可得y2=(1-
),
∴
+
=
×2=
.
当l与x轴不垂直时,设直线l的参数方程为
(t为参数),代入椭圆方程可得:(1+sin2θ)t2+2tx0cosθ+
-2=0,
t1+t2=-
,t1t2=
.
∴
+
=
+
=
=
=
=
.
令4
=-(2
-4),解得
=
.
此式=
=3.
此时
=3.
因此存在一定点 E(
,0)(0<
<
),使得当过点 E的直线l与曲线C相交于 A,B两点时,
+
为定值3.
| x2 |
| a2 |
| y2 |
| b2 |
∵△ADB面积的最大值为
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
联立
|
| 2 |
∴椭圆C的方程为
| x2 |
| 2 |
(2)假设存在一定点 E(x0,0)(0<x0<
| 2 |
| 1 | ||
|
|
| 1 | ||
|
|
当l⊥x轴时,把x0代入椭圆方程可得y2=(1-
| ||
| 2 |
∴
| 1 | ||
|
|
| 1 | ||
|
|
| 2 | ||
2-
|
| 4 | ||
2-
|
当l与x轴不垂直时,设直线l的参数方程为
|
| x | 2 0 |
t1+t2=-
| 2x0cosθ |
| 1+sin2θ |
| ||
| 1+sin2θ |
∴
| 1 | ||
|
|
| 1 | ||
|
|
| 1 | ||
|
| 1 | ||
|
| (t1+t2)2-2t1t2 |
| (t1t2)2 |
=
(
| ||||||
(
|
=
4
| ||||
(
|
=
4
| ||||||
(
|
令4
| x | 2 0 |
| x | 2 0 |
| x | 2 0 |
| 2 |
| 3 |
此式=
| ||||
(-
|
此时
| 4 | ||
2-
|
因此存在一定点 E(
| ||
| 3 |
| ||
| 3 |
| 2 |
| 1 | ||
|
|
| 1 | ||
|
|
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、直线的参数方程及其应用、定长问题,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
由“a>b,则a+c>b+c”推理到“a>b,则ac>bc”是( )
| A、归纳推理 | B、类比推理 |
| C、演绎推理 | D、都不是 |
正三棱锥的三视图如图所示,则其外接球的体积为( )
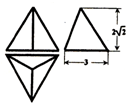

A、9
| ||||
B、
| ||||
| C、18π | ||||
| D、6π |
设函数f(x)可导,则
=( )
| lim |
| △x→0 |
| f(1+△x)-f(1) |
| △x |
| A、f′(1) |
| B、f′(x) |
| C、-f′(1) |
| D、-f′(x) |