题目内容
f(x)为R上的偶函数,若对任意的x1、x2∈(-∞,0](x1≠x2),都有
>0,则( )
| f(x2)-f(x1) |
| x2-x1 |
| A、f(-2)<f(1)<f(3) |
| B、f(1)<f(-2)<f(3) |
| C、f(3)<f(-2)<f(1) |
| D、f(3)<f(1)<f(-2) |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:先根据对任意的x1,x2∈(-∞,0](x1≠x2),都有(x2-x1)•[f(x2)-f(x1)]>0,可得函数f(x)在(-∞,0](x1≠x2)单调递增.进而可推断f(x)在[0,+∞)上单调递减,进而可判断出f(3),f(-2)和f(1)的大小.
解答:
解:∵对任意的x1、x2∈(-∞,0](x1≠x2),都有
>0,
故f(x)在x1,x2∈(-∞,0](x1≠x2)单调递增.
又∵f(x)是偶函数,
∴f(x)在[0,+∞)上单调递减,
且满足n∈N*时,f(-2)=f(2),
由3>2>1>0,
得f(3)<f(-2)<f(1),
故选:C.
| f(x2)-f(x1) |
| x2-x1 |
故f(x)在x1,x2∈(-∞,0](x1≠x2)单调递增.
又∵f(x)是偶函数,
∴f(x)在[0,+∞)上单调递减,
且满足n∈N*时,f(-2)=f(2),
由3>2>1>0,
得f(3)<f(-2)<f(1),
故选:C.
点评:本题主要考查了函数奇偶性的应用和函数的单调性的应用.属基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
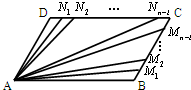 已知平行四边形ABCD,点M1,M2,M3,…,Mn-1和N1,N2,N3,…,Nn-1分别将线段BC和DC,n等分(n∈N*,n≥2),如图,若
已知平行四边形ABCD,点M1,M2,M3,…,Mn-1和N1,N2,N3,…,Nn-1分别将线段BC和DC,n等分(n∈N*,n≥2),如图,若| AM1 |
| AM2 |
| AMn-1 |
| AN1 |
| AN2 |
| ANn-1 |
| AC |
| A、29 | B、30 | C、31 | D、32 |
由“a>b,则a+c>b+c”推理到“a>b,则ac>bc”是( )
| A、归纳推理 | B、类比推理 |
| C、演绎推理 | D、都不是 |
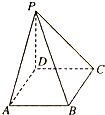 如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PD⊥底面ABCD,且PD=a,PA=PC=
如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PD⊥底面ABCD,且PD=a,PA=PC=| 2 |
(1)求证:点A在PA为直径的圆上;
(2)若在这个四棱锥内放一球,求此球的最大半径.
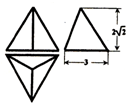
正三棱锥的三视图如图所示,则其外接球的体积为( )

A、9
| ||||
B、
| ||||
| C、18π | ||||
| D、6π |