题目内容
若双曲线
-
=1(a>0,b>0)的离心率为
,则椭圆
+
=1的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:运用离心率公式,可得双曲线的b=
a,判断椭圆的焦点在y轴上,再由离心率公式计算即可得到.
| 2 |
解答:
解:双曲线
-
=1(a>0,b>0)的离心率为
,
即为
=
,
即有b=
a,
则椭圆
+
=1的离心率为
=
=
.
故选C.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
即为
| ||
| a |
| 3 |
即有b=
| 2 |
则椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| b |
| ||
|
=
| ||
| 2 |
故选C.
点评:本题考查双曲线和椭圆的方程和性质,考查离心率的求法,属于基础题和易错题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
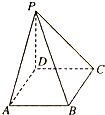 如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PD⊥底面ABCD,且PD=a,PA=PC=
如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PD⊥底面ABCD,且PD=a,PA=PC=| 2 |
(1)求证:点A在PA为直径的圆上;
(2)若在这个四棱锥内放一球,求此球的最大半径.
已知正四面体ABCD的棱长为1,则
•
=(( )
| AB |
| CD |
A、-
| ||
B、
| ||
| C、1 | ||
| D、0 |
正三棱锥的三视图如图所示,则其外接球的体积为( )
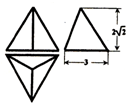

A、9
| ||||
B、
| ||||
| C、18π | ||||
| D、6π |
下列等式成立的是( )
| A、(cos2x)'=sin2x | ||||
B、
| ||||
C、
| ||||
| D、(3x)'=x•3x-1 |