题目内容
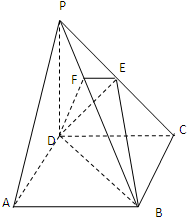 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F,求证:PF=
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F,求证:PF=| 1 |
| 3 |
考点:直线与平面垂直的性质
专题:空间位置关系与距离
分析:建立空间直角坐标系,利用EF⊥PB和F在PB上,得到向量垂直和共线,得到F的坐标,进一步得到
=
,从而得证.
| PF |
| 1 |
| 3 |
| PB |
解答:
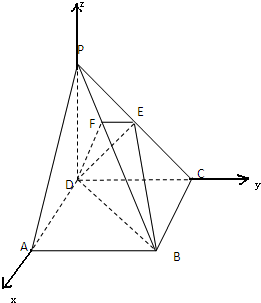 证明:建立坐标系如图:
证明:建立坐标系如图:
设正方体棱长为1,则P(0,0,1),B(1,1,0),C(0,1,0),E(0,
,
),设F(a,b,c),
所以
=(1,1,-1),
=(a,b-
,c-
),
=(a,b,c-1),
由EF⊥PB,以及F在PB上,得
•
=0,并且
=λ
,
所以a+b-c=0并且a=b=1-c,解得a=b=
,c=
,
所以
=(
,
,-
),所以
=
,
所以PF=
PB.
 证明:建立坐标系如图:
证明:建立坐标系如图:设正方体棱长为1,则P(0,0,1),B(1,1,0),C(0,1,0),E(0,
| 1 |
| 2 |
| 1 |
| 2 |
所以
| PB |
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
| PF |
由EF⊥PB,以及F在PB上,得
| EF |
| PB |
| PF |
| PB |
所以a+b-c=0并且a=b=1-c,解得a=b=
| 1 |
| 3 |
| 2 |
| 3 |
所以
| PF |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| PF |
| 1 |
| 3 |
| PB |
所以PF=
| 1 |
| 3 |
点评:本题考查了利用向量垂直和共线得到平面几何中线段关系,体现了向量的工具性.

练习册系列答案
相关题目
与角
终边相同的角是( )
| 11π |
| 6 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
函数y=
+
( )
| 3-x2 |
| 9 |
| |x|+1 |
| A、只是偶函数 |
| B、只是奇函数 |
| C、既是偶函数,又是奇函数 |
| D、是非奇非偶函数 |
若
=(-2,1,4),
=(3,2,-1)分别是直线l1,l2的方向向量,则( )
| a |
| b |
| A、l1∥l2 |
| B、l1⊥l2 |
| C、l1与l2相交 |
| D、l1与l2相交或异面 |
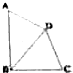 已知在四边形ABCD中,∠ABC=90°,BD平分∠ABC,∠ADC=135°,BC=8,AB=9,求CD的长.
已知在四边形ABCD中,∠ABC=90°,BD平分∠ABC,∠ADC=135°,BC=8,AB=9,求CD的长.