题目内容

若变量x，y满足约束条件
x+3y-3≥0
2x-y-3≤0
x-y+1≥0.
，则z=x+y的最大值为
 
．
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，利用z的几何意义，即可得到结论．
解答： 解：作出不等式组对应的平面区域如图：
由z=x+y得y=-x+z，
平移直线y=-x+z，
由图象可知当直线y=-x+z经过点A时，直线的截距最大，
此时z最大，
由
2x-y-3=0
x-y+1=0
，解得
x=4
y=5
，
即A（4，5），此时z=4+5=9，
故答案为：9．
点评：本题主要考查线性规划的应用，利用数形结合是解决本题的关键．
练习册系列答案
相关题目
已知动圆过定点（1，0），且与直线x=-1相切．
（1）求动圆圆心C的轨迹方程；
（2）设A、B是轨迹C上两个不同的点，且OA⊥OB，证明直线AB恒过定点，并求定点的坐标．
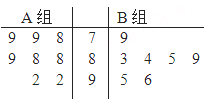天府新区的战略定位是以城乡一体化、全面现代化、充分引进国际化为引领，并以现代制造业为主，高端服务业集聚，宜业宜商宜居的国际化现代新城区，为引进优秀厂家，某企业对16家厂家根据地域分为两组，分别由A、B两组评委对各项指标进行综合评比打分，两个组队对16家厂家评比最后综合得分的茎叶图如图所示，其中茎为十位数，叶为个位数，若某厂家总和得分高于16家厂家的平均分则确定为优秀厂家．
（Ⅰ）若在确定为优秀厂家的厂家中随机抽取2家进行复查，求抽取的2家进行复查的分别是A、B组评定出的优秀厂家各1个的概率；
（Ⅱ）若从A、B两组评定出确定为优秀厂家中随机选取3家人户，记选取的3家来自B组评定出的优秀厂家数为ξ，求随机变量ξ的分布列和数学期望．
已知椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)上的顶点为A（0，5），离心率为
3
2
．
（Ⅰ）求椭圆E的方程；
（Ⅱ）若直线y=-4交椭圆E于点B，C两点（点B在点C的左侧），点D在椭圆上，且满足
BD
=m
BA
+n
BC
（m，n为实数），求m+n的最大值以及对应点D的坐标．
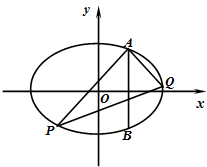如图，两条相交线段AB、PQ的四个端点都在椭圆
x2
4
+
y2
3
=1上，其中，直线AB的方程为x=m，直线PQ的方程为y=
1
2
x+n．
（Ⅰ）若n=0，∠BAP=∠BAQ，求m的值；
（Ⅱ）探究：是否存在常数m，当n变化时，恒有∠BAP=∠BAQ？
已知函数f(x)=
x
x+2
，x∈(
1
2
，1]
-
1
2
x+
1
4
，x∈[0，
1
2
]
，g(x)=asin(
π
3
x+
3π
2
)-2a+2(a＞0)，给出下列结论：
①函数f（x）的值域为[0，
1
3
]；
②函数g（x）在[0，1]上是增函数；
③对任意a＞0，方程f（x）=g（x）在[0，1]内恒有解；
④若存在x1，x2∈[0，1]，使得f（x1）=g（x2）成立，则实数a的取值范围是
5
9
≤a≤
4
5
．
其中所有正确结论的序号是
 
．
某程序框图如图所示，则程序运行后输出的S值为
 
．
某超市中秋前30天月饼销售总量f（t）与时间t（0＜t≤30，t∈Z）的关系大致满足f（t）=t2+10t+12，则该超市前t天平均售出（如前10天的平均售出为
f(10)
10
）的月饼最少为
 
．
给出下列四个命题：
①?x∈R，x2+2＞0
②?x∈N，x4≥1
③?x0∈Z，x03＜1
④?x0∈Q，x02=3
其中是真命题是（　　）
A、①②B、④①C、③④D、③①

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网