��Ŀ����
��֪����f(x)=
��g(x)=asin(
x+
)-2a+2(a��0)���������н��ۣ�
�ٺ���f��x����ֵ��Ϊ[0��
]��
�ں���g��x����[0��1]������������
�۶�����a��0������f��x��=g��x����[0��1]�ں��н⣻
��������x1��x2��[0��1]��ʹ��f��x1��=g��x2����������ʵ��a��ȡֵ��Χ��
��a��
��
����������ȷ���۵������ ��
|
| �� |
| 3 |
| 3�� |
| 2 |
�ٺ���f��x����ֵ��Ϊ[0��
| 1 |
| 3 |
�ں���g��x����[0��1]������������
�۶�����a��0������f��x��=g��x����[0��1]�ں��н⣻
��������x1��x2��[0��1]��ʹ��f��x1��=g��x2����������ʵ��a��ȡֵ��Χ��
| 5 |
| 9 |
| 4 |
| 5 |
����������ȷ���۵������
���㣺���������ж���Ӧ��
ר�⣺���������ʼ�Ӧ��
�������ٵ�x��(
��1]ʱ������f��x��=
=1-
�����������ɵ�f(
)��f(x)��f(1)��
��x��[0��
]ʱ������f��x��=-
x+
������һ�κ����ĵ����Կɵ�f(
)��f(x)��f(0)��
���ɵõ�����f��x����ֵ��
�������յ���ʽ�ɵ�g��x��=-acos
x-2a+2���������Һ����ĵ����ԣ������ó�g��x����[0��1]�ϵ����ԣ�
���ɢڿ�֪��g��0����g��x����g��1����������a��0������f��x��=g��x����[0��1]�ں��н⣬
���������f��x����ֵ��[0��
]⊆{g��x��|x��[0��1]}������ж����ɣ�
�ܴ���x1��x2��[0��1]��ʹ��f��x1��=g��x2����������
������ɣ�
| 1 |
| 2 |
| x |
| x+2 |
| 2 |
| x+2 |
| 1 |
| 2 |
��x��[0��
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
���ɵõ�����f��x����ֵ��
�������յ���ʽ�ɵ�g��x��=-acos
| �� |
| 3 |
���ɢڿ�֪��g��0����g��x����g��1����������a��0������f��x��=g��x����[0��1]�ں��н⣬
���������f��x����ֵ��[0��
| 1 |
| 3 |
�ܴ���x1��x2��[0��1]��ʹ��f��x1��=g��x2����������
|
���
�⣺�ٵ�x��(
��1]ʱ��f��x��=
=1-
������������f(
)��f(x)��f(1)����
��f(x)��
��
��x��[0��
]ʱ���ɺ���f��x��=-
x+
�����ݼ�����f(
)��f(x)��f(0)����0��f(x)��
��
�ຯ��f��x����ֵ��Ϊ[0��
]����ˢ���ȷ��
��g��x��=-acos
x-2a+2����x��[0��1]����0��
��
�����cos
��[0��1]�ϵ����ݼ���
��a��0����g��x����[0��1]�ϵ��������������ȷ��
���ɢڿ�֪��g��0����g��x����g��1������-3a+2��g(x)��-
a+2��
������a��0������f��x��=g��x����[0��1]�ں��н⣬
���������f��x����ֵ��[0��
]⊆{g��x��|x��[0��1]}��
��-3a+2��0��-
a+2��
�����a=
����ˢ۲���ȷ��
�ܴ���x1��x2��[0��1]��ʹ��f��x1��=g��x2����������
�ɢۿ�֪��g(x)max=g(1)=-
a+2��g��x��min=g��0��=-3a+2��
��-3a+2��
��-
a+2��0�����
��a��
��
��ʵ��a��ȡֵ��Χ��
��a��
����ȷ��
���Ͽ�֪��ֻ�Т٢ڢ���ȷ��
�ʴ�Ϊ���٢ڢܣ�
| 1 |
| 2 |
| x |
| x+2 |
| 2 |
| x+2 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 3 |
��x��[0��
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
�ຯ��f��x����ֵ��Ϊ[0��
| 1 |
| 3 |
��g��x��=-acos
| �� |
| 3 |
| ��x |
| 3 |
| �� |
| 3 |
| ��x |
| 3 |
��a��0����g��x����[0��1]�ϵ��������������ȷ��
���ɢڿ�֪��g��0����g��x����g��1������-3a+2��g(x)��-
| 5 |
| 2 |
������a��0������f��x��=g��x����[0��1]�ں��н⣬
���������f��x����ֵ��[0��
| 1 |
| 3 |
��-3a+2��0��-
| 5 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
�ܴ���x1��x2��[0��1]��ʹ��f��x1��=g��x2����������
|
�ɢۿ�֪��g(x)max=g(1)=-
| 5 |
| 2 |
��-3a+2��
| 1 |
| 3 |
| 5 |
| 2 |
| 5 |
| 9 |
| 4 |
| 5 |
��ʵ��a��ȡֵ��Χ��
| 5 |
| 9 |
| 4 |
| 5 |
���Ͽ�֪��ֻ�Т٢ڢ���ȷ��
�ʴ�Ϊ���٢ڢܣ�
�����������ۺϿ����˷ֶκ����ĵ����ԡ����������ĵȼ�ת�������Ȼ���֪ʶ��������ܷ����������˷�������ͽ��������������������⣮

��ϰ��ϵ�д�
�����Ŀ
��F1��F2Ϊ��Բ����
+
=1��a��b��0�������ҽ��㣬��M����Բ���ϣ�����MF1F2Ϊֱ�������Σ���|MF1|=2|MF2|������Բ����������Ϊ��������
| x2 |
| a2 |
| y2 |
| b2 |
A��
| ||||||||
B��
| ||||||||
C��
| ||||||||
D��
|
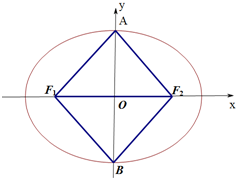 ��ͼ������ԲC��
��ͼ������ԲC��