题目内容
已知椭圆E:
+
=1(a>b>0)上的顶点为A(0,5),离心率为
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)若直线y=-4交椭圆E于点B,C两点(点B在点C的左侧),点D在椭圆上,且满足
=m
+n
(m,n为实数),求m+n的最大值以及对应点D的坐标.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆E的方程;
(Ⅱ)若直线y=-4交椭圆E于点B,C两点(点B在点C的左侧),点D在椭圆上,且满足
| BD |
| BA |
| BC |
考点:直线与圆锥曲线的关系,椭圆的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据顶点为A(0,5),离心率为
,求出几何量,尽快求椭圆E的方程;
(Ⅱ)设P(x,y),根据
=m
+n
(m,n为实数),可得x=6m+12n-6,y=9m+8n-4,进而可得m+n,利用三角换元,可求m+n的最大值以及对应点D的坐标.
| ||
| 2 |
(Ⅱ)设P(x,y),根据
| BD |
| BA |
| BC |
解答:
解:(I)由题意得:在椭圆E中,b=5,且e=
=
=
,a2=b2+c2,
∴a2=100,
∴椭圆E的方程为:
+
=1…(4分)
(II)将y=-4代入椭圆方程
+
=1中得x2=36,∴x=±6,
∵B点在C点左侧,∴B(-6,-4),C(6,-4).
∵A(0,5),∴
=(6,9),
=(12,0),
设D点(x,y),则
=(x+6,y+4)
∵
=m
+n
,即x+6=6m+12n,y+4=9m,
整理可得m=
,n=
…(7分)
∴m+n=
;
令t=3x+2y,与椭圆方程,消去y整理方程得:满足△≥0,则t≤10
;…(10分)
∴m+n的最大值为
=
,即3x+2y=10
时满足…(11分)
而
⇒
,
∴D(3
,
)…(13分)
| c |
| a |
1-
|
| ||
| 2 |
∴a2=100,
∴椭圆E的方程为:
| x2 |
| 100 |
| y2 |
| 25 |
(II)将y=-4代入椭圆方程
| x2 |
| 100 |
| y2 |
| 25 |
∵B点在C点左侧,∴B(-6,-4),C(6,-4).
∵A(0,5),∴
| BA |
| BC |
设D点(x,y),则
| BD |
∵
| BD |
| BA |
| BC |
整理可得m=
| y+4 |
| 9 |
| 3x-2y+10 |
| 36 |
∴m+n=
| 3x+2y+26 |
| 36 |
令t=3x+2y,与椭圆方程,消去y整理方程得:满足△≥0,则t≤10
| 10 |
∴m+n的最大值为
10
| ||
| 36 |
5
| ||
| 18 |
| 10 |
而
|
|
∴D(3
| 10 |
| ||
| 2 |
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查向量知识的运用,解题的关键是确定坐标之间的关系,属于中档题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
已知存在正数a,b,c满足
≤
≤2,clnb=a+clnc,则ln
的取值范围是( )
| 1 |
| e |
| c |
| a |
| b |
| a |
A、[1,
| ||
| B、[1,+∞) | ||
| C、(-∞,e-1] | ||
| D、[1,e-1] |
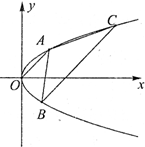 已知点A,B,C是抛物线L:y2=2px(p>0)上的不同的三点,O为坐标原点,直线OA∥BC,且抛物线L的准线方程为x=-1.
已知点A,B,C是抛物线L:y2=2px(p>0)上的不同的三点,O为坐标原点,直线OA∥BC,且抛物线L的准线方程为x=-1.