题目内容
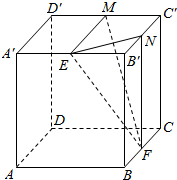 在正方体ABCD-A′B′C′D′中,E,F,M,N分别是A′B′,BC,C′D′,B′C′的中点.
在正方体ABCD-A′B′C′D′中,E,F,M,N分别是A′B′,BC,C′D′,B′C′的中点.(1)求证:平面MNF⊥平面ENF.
(2)求二面角M-EF-N的余弦值.
考点:与二面角有关的立体几何综合题,平面与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)欲证平面MNF⊥平面ENF,先证直线与平面垂直,由题意可得:MN⊥EN,MN⊥NF,所以MN⊥面ENF,进一步易得平面MNF⊥平面ENF;
(2)求出S△MEF=
•2•
=
,S△NEF═
•2•
=
,即可求出二面角M-EF-N的余弦值.
(2)求出S△MEF=
| 1 |
| 2 |
| 6-1 |
| 5 |
| 1 |
| 2 |
| 2 |
| 2 |
解答:
 (1)证明:连接A′C′,B′D′
(1)证明:连接A′C′,B′D′
∵E,M,N分别是A′B′,C′D′,B′C′的中点,
∴MN∥B′D′,EN∥A′C′
又∵A′C′⊥B′D′
∴MN⊥EN
在正方体ABCD-A′B′C′D′中,
∵F,N分别是BC,B′C′的中点,
∴NF∥B′B
又∵B1B⊥面A′B′C′D′,∴NF⊥面A1B1C1D1
∵MN?面A′B′C′D′
∴MN⊥NF
∵EN∩NF=N
∴MN⊥面ENF
又∵MN?平面MNF
∴平面MNF⊥平面ENF
(2)解:设正方体的棱长为2,则
△MEF中,ME=2,EF=
,MF=
,∴S△MEF=
•2•
=
,
△EFN中,NE=
,NF=2,EF=
,∴S△NEF═
•2•
=
,
∴二面角M-EF-N的余弦值为
=
.
 (1)证明:连接A′C′,B′D′
(1)证明:连接A′C′,B′D′∵E,M,N分别是A′B′,C′D′,B′C′的中点,
∴MN∥B′D′,EN∥A′C′
又∵A′C′⊥B′D′
∴MN⊥EN
在正方体ABCD-A′B′C′D′中,
∵F,N分别是BC,B′C′的中点,
∴NF∥B′B
又∵B1B⊥面A′B′C′D′,∴NF⊥面A1B1C1D1
∵MN?面A′B′C′D′
∴MN⊥NF
∵EN∩NF=N
∴MN⊥面ENF
又∵MN?平面MNF
∴平面MNF⊥平面ENF
(2)解:设正方体的棱长为2,则
△MEF中,ME=2,EF=
| 6 |
| 6 |
| 1 |
| 2 |
| 6-1 |
| 5 |
△EFN中,NE=
| 2 |
| 6 |
| 1 |
| 2 |
| 2 |
| 2 |
∴二面角M-EF-N的余弦值为
| ||
|
| ||
| 5 |
点评:本小题主要考查空间线面关系,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力

练习册系列答案
相关题目
 如图,在Rt△ABC中,已知BC=5,AB=3,AC=4,若长为10的线段PQ以点A为中点,问
如图,在Rt△ABC中,已知BC=5,AB=3,AC=4,若长为10的线段PQ以点A为中点,问