题目内容
正四棱锥P-ABCD的底面边长是2，侧棱长是
，且它的五个顶点都在同一个球面上，则此球的半径是（ ）
| 6 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、3 |
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：设球半径为R，底面中心为O'且球心为O．正四棱锥P-ABCD中根据AB=2且PA=
，算出AO'=
、PO'=2、OO'=2-R，在Rt△AOO′中利用勾股定理建立关于R的等式，解出R=
．
| 6 |
| 2 |
| 3 |
| 2 |
解答：
解：如图所示，设球半径为R，底面中心为O'且球心为O，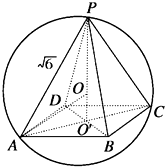
∵正四棱锥P-ABCD中AB=2，PA=
，
∴AO'=
AB=
，可得PO'═2，OO'=PO'-PO=2-R．
∵在Rt△AOO'中，AO2=AO'2+OO'2，
∴R2=（
）2+（2-R）2，解之得R=
，
故选：C．
∵正四棱锥P-ABCD中AB=2，PA=
| 6 |
∴AO'=
| ||
| 2 |
| 2 |
∵在Rt△AOO'中，AO2=AO'2+OO'2，
∴R2=（
| 2 |
| 3 |
| 2 |
故选：C．
点评：本题给出正四棱锥的形状，求它的外接球的半径，着重考查了正棱锥的性质、多面体的外接球、勾股定理等知识，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
如图，AB和BC分别与圆O相切于点D、C，AC经过圆心O，且BC=2OC=4，则AD=把函数f（x）=sin（-2x+
）的图象向右平移φ（0＜φ＜π）个单位可以得到函数g（x）的图象，若g（x）为偶函数，则φ的值为（ ）
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中，若a2+c2-b2=-ac，则角B=（ ）
| A、120° | B、60° |
| C、135° | D、150° |
已知连续函数y=f（x），有f（a）f（b）＜0 ）（a＜b），则y=f（x）（ ）
| A、在区间[a，b]上可能没有零点 |
| B、在区间[a，b]上至少有一个零点 |
| C、在区间[a，b]上零点个数为奇数个 |
| D、在区间[a，b]上零点个数为偶数个 |
已知集合M={x|-1＜x-a＜2}，N={x|x2≥x}，若M∪N=R，则实数a的取值范围是（ ）
| A、（-1，1） |
| B、[-1，1） |
| C、[-1，1] |
| D、（-1，1] |
在△ABC中，∠A、∠B、∠C所对的边长分别是4、
，2则cosA的值为（ ）
| 7 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
若函数f（x）如表所示：
则f[f（1）]=（ ）
| x | 0 | 1 | 2 | 3 |
| f（x） | 3 | 2 | 1 | 0 |
| A、0 | B、1 | C、2? | D、3 |