题目内容
17.已知长方体有一个公共顶点的三个面的面积分别是$\sqrt{3}$,$\sqrt{5}$,$\sqrt{15}$.则长方体的体积是多少.分析 根据已知的长方体相交于一个顶点的三个面的面积即可求出相邻三边长度,从而根据长方体的体积公式求出该长方体的体积.
解答 解:长方体有一个公共顶点的三个面的面积分别是$\sqrt{3}$,$\sqrt{5}$,$\sqrt{15}$.
设长方体相邻三边长分别为:x,y,z;则xy=$\sqrt{3}$,xz=$\sqrt{5}$,yz=$\sqrt{15}$.解得x=1,y=$\sqrt{3}$,z=$\sqrt{5}$.
∴该长方体的体积为1×$\sqrt{3}$×$\sqrt{5}$=$\sqrt{15}$.
故答案为:$\sqrt{15}$.
点评 考查长方体各面的特点,以及长方体的体积公式.

练习册系列答案
相关题目
7.某几何体的三视图如图所示,则该几何体的体积等于( )


| A. | 6+6π | B. | 6+8π | C. | 8+6π | D. | 8+8π |
5.若$A({3,\frac{π}{3}})$,$B({3,\frac{7π}{6}})$,则△AOB的面积为( )
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | 3 | C. | $\frac{9}{4}$ | D. | 9 |
2.在抛物线y=x2与直线y=2围成的封闭图形内任取一点A,O为坐标原点,则直线OA被该封闭图形解得的线段长小于$\sqrt{2}$的概率是( )
| A. | $\frac{{\sqrt{3}}}{15}$ | B. | $\frac{{\sqrt{3}}}{16}$ | C. | $\frac{{\sqrt{2}}}{16}$ | D. | $\frac{{\sqrt{2}}}{14}$ |
6.在△ABC中,角A,B,C的对边分别为a,b,c,若a=2,b=sinA+cosA=$\sqrt{2}$,则△ABC的面积为( )
| A. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}+1}{4}$ | D. | $\frac{\sqrt{3}+1}{2}$ |
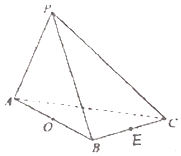 在三棱锥P-ABC中,△PAC和△PBC是边长为$\sqrt{2}$的等边三角形,AB=2,O是AB中点,E是BC中点.
在三棱锥P-ABC中,△PAC和△PBC是边长为$\sqrt{2}$的等边三角形,AB=2,O是AB中点,E是BC中点. 如图,我校计划建一个面积为200m2的矩形场地,要求矩形场地的一面利用旧墙(旧墙需要维修),其余三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为41元/米,新墙的造价为400元/米.设利用旧墙的长度为x(单位:米),修建此矩形场地围墙的总费用y(单位:元).
如图,我校计划建一个面积为200m2的矩形场地,要求矩形场地的一面利用旧墙(旧墙需要维修),其余三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为41元/米,新墙的造价为400元/米.设利用旧墙的长度为x(单位:米),修建此矩形场地围墙的总费用y(单位:元).