题目内容
12．
如图，我校计划建一个面积为200m2的矩形场地，要求矩形场地的一面利用旧墙（旧墙需要维修），其余三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，已知旧墙的维修费用为41元/米，新墙的造价为400元/米．设利用旧墙的长度为x（单位：米），修建此矩形场地围墙的总费用y（单位：元）．（1）将y表示为x的函数；
（2）求当x为何值时，y取得最小值，并求出此最小值．
分析 （1）利用已知条件列出函数的解析式即可．
（2）利用基本不等式求解函数的最值即可．
解答 解：（1）由题意得矩形场地的另一边长为$\frac{200}{x}$米，
∴y=41x+（x+2×$\frac{200}{x}-2$）×400=441x+$\frac{160000}{x}$-800，（x＞0）．
（2）由（1）得y=441x+$\frac{160000}{x}$-800≥2$\sqrt{441x•\frac{160000}{x}}$-800=16000，
当且仅当441x=$\frac{160000}{x}$，即x=$\frac{400}{21}$时，等号成立，
即当x=$\frac{400}{21}$时，y取得最小值16000元．
点评 本题考查函数的实际应用，基本不等式的应用，考查转化思想以及计算能力．
练习册系列答案
相关题目
3．已知函数$f（x）=\frac{1}{3}{x^3}-{x^2}+ax-5$在[-1，2]上不单调，则实数a的取值范围是（ ）
| A． | [-3，1） | B． | （-3，0） | C． | （-3，1） | D． | （-3，1] |
7．已知数列{an}满足a1=60，an+1-an=2n，则$\frac{{a}_{n}}{n}$的最小值为（ ）
| A． | $\frac{29}{2}$ | B． | 2$\sqrt{60}$ | C． | $\frac{29}{4}$ | D． | $\frac{102}{7}$ |
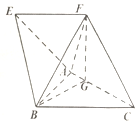如图，在四棱锥A-BCFE中，四边形EFCB为梯形，EF∥BC，且EF=$\frac{3}{4}$BC，△ABC是边长为2的正三角形，顶点F在AC上的射影为点G，且FG=$\sqrt{3}$，CF=$\frac{{\sqrt{21}}}{2}$，BF=$\frac{5}{2}$．
2．如果随机变量ξ～B（6，$\frac{1}{2}$），则P（ξ=3）的值为（ ）
| A． | $\frac{5}{16}$ | B． | $\frac{5}{8}$ | C． | $\frac{3}{16}$ | D． | $\frac{7}{16}$ |