题目内容
16.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知sinA-sinB=$\frac{1}{3}$sinC,3b=2a,2≤a2+ac≤18,设△ABC的面积为S,p=$\sqrt{2}$a-S,则p的最大值是$\frac{9\sqrt{2}}{8}$.分析 根据题意,利用正弦定理求得a、b、c的关系,以及a的取值范围,再利用余弦定理求得cosB、sinB 的值,从而求得△ABC的面积S,写出p的解析式,利用二次函数的性质即可求得p的最大值.
解答 解:△ABC中,由sinA-sinB=$\frac{1}{3}$sinC,
利用正弦定理得c=3a-3b,
再根据3b=2a,2≤a2+ac≤18,
可得c=a,b=$\frac{2a}{3}$,1≤a≤3.
由余弦定理得 b2=$\frac{4{a}^{2}}{9}$=a2+a2-2a•a•cosB,
求得cosB=$\frac{7}{9}$,
∴sinB=$\frac{4\sqrt{2}}{9}$,
∴△ABC的面积为S=$\frac{1}{2}$•ac•sinB=$\frac{1}{2}$a2•$\frac{4\sqrt{2}}{9}$=$\frac{2\sqrt{2}}{9}$•a2,
故p=$\sqrt{2}$a-S=$\sqrt{2}$a-$\frac{2\sqrt{2}}{9}$a2=$\frac{9\sqrt{2}}{8}$-$\frac{2\sqrt{2}}{9}$(a-$\frac{9}{4}$)2,
利用二次函数的性质结合a的范围1≤a≤3,可得:
当a=$\frac{9}{4}$时,p取得最大值是$\frac{9\sqrt{2}}{8}$.
故答案为:$\frac{9\sqrt{2}}{8}$.
点评 本题主要考查了正弦定理和余弦定理的应用问题,也考查了二次函数的最值问题,是综合性题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知数列{an}中,a1=1,a2=3,an+2+an=an+1,则a2014=( )
| A. | -3 | B. | -1 | C. | 2 | D. | 3 |
1.已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左、右焦点分别为F1,F2,过F1的直线l交椭圆与两点A,B,则|AF2|+|BF2|的最大值为( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
8.正项等比数列{an}中,a6=a5+2a4,若存在两项am,an使得$\sqrt{{a_m}{a_n}}$=4a1,则$\frac{1}{m}$+$\frac{2}{n}$的最小值是( )
| A. | $\frac{{3+2\sqrt{2}}}{6}$ | B. | 1 | C. | $\frac{11}{5}$ | D. | $\frac{5}{4}$ |
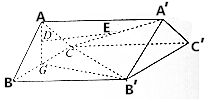 已知正三棱柱ABC-A′B′C′如图所示,其中G是BC的中点,D,E分别在线段AG,A′C上运动,使得DE∥平面BCC′B′,CC′=2BC=4.
已知正三棱柱ABC-A′B′C′如图所示,其中G是BC的中点,D,E分别在线段AG,A′C上运动,使得DE∥平面BCC′B′,CC′=2BC=4.