题目内容
7.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-4,x≤0}\\{{e}^{x}-5,x>0}\end{array}\right.$若关于x的方程|f(x)|-ax-5=0恰有三个不同的实数解,则满足条件的所有实数a的取值集合为{-e,-$\frac{5}{ln5}$,2,$\frac{5}{2}$}.分析 作出y=|f(x)|的函数图象,根据直线y=ax+5与y=|f(x)|有3个交点得出两函数图象的关系,从而得出a的值.
解答 解:令f(x)=0得x=-2或x=ln5,
∵f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
∴|f(x)|=$\left\{\begin{array}{l}{{x}^{2}-4,x≤-2}\\{4-{x}^{2},-2<x≤0}\\{5-{e}^{x},0<x<ln5}\\{{e}^{x}-5,x>ln5}\end{array}\right.$,
作出y=|f(x)|的函数图象如图所示:
∵关于x的方程|f(x)|-ax-5=0恰有三个不同的实数解,
∴直线y=ax+5与y=|f(x)|有3个交点,
∴y=ax+5过点(-2,0)或过点(ln5,0)或y=ax+5与y=|f(x)|的图象相切,
(1)若y=ax+5过点(-2,0),则a=$\frac{5}{2}$,
(2)若y=ax+5过点(ln5,0),则a=-$\frac{5}{ln5}$,
(3)若y=ax+5与y=|f(x)|在(-2,0)上的图象相切,设切点为(x0,y0),
则$\left\{\begin{array}{l}{-2{x}_{0}=a}\\{{y}_{0}=a{x}_{0}+5}\\{{y}_{0}=4-{{x}_{0}}^{2}}\end{array}\right.$,解得a=2,
(4)若y=ax+5与y=|f(x)|在(0,ln5)上的图象相切,设切点为(x1,y1),
则$\left\{\begin{array}{l}{-{e}^{{x}_{1}}=a}\\{{y}_{1}=a{x}_{1}+5}\\{{y}_{1}=5-{e}^{{x}_{1}}}\end{array}\right.$,解得a=-e,
∴a的取值集合为{-e,-$\frac{5}{ln5}$,2,$\frac{5}{2}$}.
故答案为{-e,-$\frac{5}{ln5}$,2,$\frac{5}{2}$}.
点评 本题考查了函数零点与函数图象的关系,数学结合法与分类讨论思想,属于中档题.

| A. | (-∞,-1) | B. | (2,+∞) | C. | (0,2) | D. | (-1,+∞) |
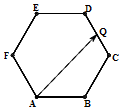
| A. | $\overrightarrow{AB}•\overrightarrow{AQ}$ | B. | $\overrightarrow{AC}•\overrightarrow{AQ}$ | C. | $\overrightarrow{AD}•\overrightarrow{AQ}$ | D. | $\overrightarrow{AE}•\overrightarrow{AQ}$ |
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
| A. | b<a<c | B. | c<b<a | C. | c<a<b | D. | b<c<a |
| A. | $\frac{5}{2}$或$\frac{3}{2}$ | B. | $\frac{3}{2}$或1 | C. | 1或$\frac{1}{2}$ | D. | $\frac{1}{2}$或$\frac{5}{2}$ |
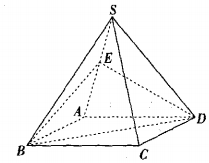 如图,四棱锥S-ABCD中,底面ABCD为平行四边形,E是SA的上一点,当点E满足条件SE=EA,时,SC∥平面EBD,写出条件并加以证明.
如图,四棱锥S-ABCD中,底面ABCD为平行四边形,E是SA的上一点,当点E满足条件SE=EA,时,SC∥平面EBD,写出条件并加以证明.