题目内容

16．设a=（$\frac{9}{7}$）${\;}^{-\frac{1}{4}}$，b=（$\frac{9}{7}$）${\;}^{\frac{1}{3}}$，c=log3$\frac{7}{9}$，则a，b，c的大小关系是（　　）
A．b＜a＜cB．c＜b＜aC．c＜a＜bD．b＜c＜a

分析 运用对数函数的单调性，可得c＜0，再由指数函数的单调性，可得a＜b，进而得到结论．

解答 解：c=log3$\frac{7}{9}$＜log31=0，
由y=（$\frac{9}{7}$）x在R上为增函数，
-$\frac{1}{4}$＜$\frac{1}{3}$，
可得0＜（$\frac{9}{7}$）${\;}^{-\frac{1}{4}}$＜（$\frac{9}{7}$）${\;}^{\frac{1}{3}}$，
则c＜a＜b．
故选：C．

点评 本题考查指数函数和对数函数的单调性的运用：比较函数值的大小，考查运算能力，属于基础题．

练习册系列答案
相关题目
13．设函数f（x）=$\left\{\begin{array}{l}{\frac{4}{x}+1，x≥4}\\{lo{g}_{2}x，0＜x＜4}\end{array}\right.$若f（a）=f（b）=c，f′（b）＜0，则a，b，c的大小关系是b＞a＞c．
7．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-4，x≤0}\\{{e}^{x}-5，x＞0}\end{array}\right.$若关于x的方程|f（x）|-ax-5=0恰有三个不同的实数解，则满足条件的所有实数a的取值集合为{-e，-$\frac{5}{ln5}$，2，$\frac{5}{2}$}．
4．如图，在直三棱柱ABC-A1B1C1中，AA1=BC=AC=2，AB=2$\sqrt{2}$，D、E分别是的AB，BB1的中点．
（Ⅰ）证明：BC1∥平面A1CD；
（Ⅱ）求二面角D-A1C-E的正弦值．
11．抛物线y2=4x的焦点到双曲线$\frac{{x}^{2}}{{3}^{\;}}$-y2=1的渐近线的距离是（　　）
A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{2}$C．1D．$\sqrt{3}$
1．函数$f（x）=\frac{bx+c}{{a{x^2}+1}}（a，b，c∈R）$是奇函数，且f（-2）≤f（x）≤f（2），则a=$\frac{1}{4}$．
8．设变量x，y满足约束条件$\left\{\begin{array}{l}x+2y-4≤0\\ 3x+y-3≥0\\ x-y-1≤0\end{array}\right.$，则$z=\frac{y}{x+1}$的最大值为（　　）
A．$\frac{9}{7}$B．$\frac{1}{3}$C．0D．2
5．在三棱锥P-ABC中，PA⊥平面ABC，PA=2，BC=$\sqrt{2}$，又∠BAC=135°，则该三棱锥外接球的表面积为（　　）
A．2πB．4πC．6πD．8π
6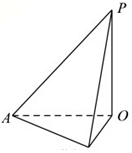．如图，有一建筑物OP，为了测量它的高度，在地面上选一长度为40m的基线AB，若在点A处测得P点的仰角为30°，在B点处的仰角为45°，且∠AOB=30°，则建筑物的高度为（　　）
A．20mB．20$\sqrt{2}$mC．20$\sqrt{3}$mD．40m

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网