题目内容
19.已知O为平面直角坐标系的原点,F2为双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,过双曲线左顶点A,做两渐近线的平行线分别与y轴交于C、D两点,B为双曲线的右顶点,若以O为圆心,|OF2|为直径的圆是四边形ACBD的内切圆,则装曲线的离心率为,( )| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 先根据双曲线的几何性质可推断出直线AD的方程,进而利用直线AD与四边形ACBD的内切圆相切,结合点到直线的距离公式得到a,b关系,最后求得a和c的关系式,即双曲线的离心率.
解答 解:由题意得:A(-a,0),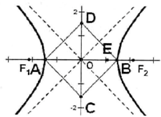 渐近线方程为y=±$\frac{b}{a}$x,
渐近线方程为y=±$\frac{b}{a}$x,
直线AD的方程为:y=$\frac{b}{a}$(x+a),
即:bx-ay+ab=0,
因为直线AD与四边形ACBD的内切圆相切,
设内切圆的半径为r,
故r=d,即$\frac{c}{2}$=$\frac{|ab|}{\sqrt{{a}^{2}+{b}^{2}}}$?a=b,
∴双曲线的离心率为e=$\frac{c}{a}$=$\sqrt{1+(\frac{b}{a})^{2}}$=$\sqrt{2}$.
故选:B.
点评 本题主要考查了双曲线的简单性质.涉及求双曲线的离心率问题,解题的关键是找到a,b和c的关系,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知sinα•cosα=$\frac{1}{8}$,且0<α<$\frac{π}{4}$,则sinα-cosα=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{4}$ | D. | -17 |
11.抛物线y2=4x的焦点到双曲线$\frac{{x}^{2}}{{3}^{\;}}$-y2=1的渐近线的距离是( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
8.设变量x,y满足约束条件$\left\{\begin{array}{l}x+2y-4≤0\\ 3x+y-3≥0\\ x-y-1≤0\end{array}\right.$,则$z=\frac{y}{x+1}$的最大值为( )
| A. | $\frac{9}{7}$ | B. | $\frac{1}{3}$ | C. | 0 | D. | 2 |
9.若a<b<0,那么下列不等式成立的是( )
| A. | ab<b2 | B. | a2<b2 | C. | lg(-ab)<lg(-a2) | D. | 2${\;}^{\frac{1}{b}}$<2${\;}^{\frac{1}{a}}$ |
 三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明,下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实,图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实,黄实,利用2×勾×股+(股-勾)2=4×朱实+黄实=弦实,化简,得勾2+股2=弦2,设勾股中勾股比为1:$\sqrt{3}$,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明,下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实,图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实,黄实,利用2×勾×股+(股-勾)2=4×朱实+黄实=弦实,化简,得勾2+股2=弦2,设勾股中勾股比为1:$\sqrt{3}$,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( ) 如图,在直三棱柱ABC-A1B1C1中,AA1=BC=AC=2,AB=2$\sqrt{2}$,D、E分别是的AB,BB1的中点.
如图,在直三棱柱ABC-A1B1C1中,AA1=BC=AC=2,AB=2$\sqrt{2}$,D、E分别是的AB,BB1的中点.