题目内容
1.袋中有2个黄球3个白球,甲乙两人分别从中任取一球,取得黄球得1分,取得白球得2分,两人总分和为X,则X=3的概率是$\frac{3}{5}$.分析 利用相互独立事件概率乘法公式、互斥事件概率加法公式求解.
解答 解:当X=3时,甲取到黄球,乙取到白球或甲取到白球,乙取到黄球,
故P(X=3)=$\frac{2}{5}×\frac{3}{4}+\frac{3}{5}×\frac{2}{4}$=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题考查概率的求法,考查相互独立事件概率乘法公式、互斥事件概率加法公式等基础知识,考查推理论证能力、运算求解能力、数据处理能力,考查化归与转化思想,函数与方程思想、数形结合思想,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知e为自然对数的底,a=($\frac{2}{e}$)-0.3,b=($\frac{e}{2}$)0.4,c=log${\;}_{\frac{2}{e}}$e,则a,b,c的大小关系是( )
| A. | c<b<a | B. | c<a<b | C. | b<a<c | D. | a<b<c |
9.已知集合A={x∈Z|x2-4x-5<0},B={x|4x>2m},若A∩B有三个元素,则实数m的取值范围是( )
| A. | [3,6) | B. | [1,2) | C. | [2,4) | D. | (2,4] |
16.已知抛物线C:y2=2px(p>0)的焦点为F,点M(x0,4)是抛物线C上一点,以M为圆心,|MF|为半径的圆被直线x=-1截得的弦长为2$\sqrt{7}$,则|MF|等于( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
10.17世纪日本数学家们对这个数学关于体积方法的问题还不了解,他们将体积公式“V=kD3”中的常数k称为“立圆术”或“玉积率”,创用了求“玉积率”的独特方法“会玉术”,其中,D为直径,类似地,对于等边圆柱(轴截面是正方形的圆柱叫做等边圆柱)、正方体也有类似的体积公式V=kD3,其中,在等边圆柱中,D表示底面圆的直径;在正方体中,D表示棱长,假设运用此“会玉术”,求得的球、等边圆柱、正方体的“玉积率”分别为k1,k2,k3=( )
| A. | $\frac{π}{4}$:$\frac{π}{6}$:1 | B. | $\frac{π}{6}$:$\frac{π}{4}$:2 | C. | 1:3:$\frac{12}{π}$ | D. | 1:$\frac{3}{2}$:$\frac{6}{π}$ |
11.某研究性学习小组调查研究性别对喜欢吃甜食的影响,部分统计数据如表:
附表:
经计算K2=10,则下列选项正确的是( )
| 女生 | 男生 | 合计 | |
| 喜欢吃甜食 | 8 | 4 | 12 |
| 不喜欢吃甜食 | 2 | 16 | 18 |
| 合计 | 10 | 20 | 30 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 有99.5%的把握认为性别对喜欢吃甜食无影响 | |
| B. | 有99.5%的把握认为性别对喜欢吃甜食有影响 | |
| C. | 有99.9%的把握认为性别对喜欢吃甜食无影响 | |
| D. | 有99.9%的把握认为性别对喜欢吃甜食有影响 |
 如图,在四棱锥P-ABCD中,底面ABCD为菱形,PC⊥平面ABCD,点E在棱PA上.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,PC⊥平面ABCD,点E在棱PA上.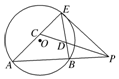 如图,A,B,E是⊙O上的点,过E点的⊙O的切线与直线AB交于点P,∠APE的平分线和AE,BE分别交于点C,D.求证:
如图,A,B,E是⊙O上的点,过E点的⊙O的切线与直线AB交于点P,∠APE的平分线和AE,BE分别交于点C,D.求证: