题目内容
11.某研究性学习小组调查研究性别对喜欢吃甜食的影响,部分统计数据如表:| 女生 | 男生 | 合计 | |
| 喜欢吃甜食 | 8 | 4 | 12 |
| 不喜欢吃甜食 | 2 | 16 | 18 |
| 合计 | 10 | 20 | 30 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 有99.5%的把握认为性别对喜欢吃甜食无影响 | |
| B. | 有99.5%的把握认为性别对喜欢吃甜食有影响 | |
| C. | 有99.9%的把握认为性别对喜欢吃甜食无影响 | |
| D. | 有99.9%的把握认为性别对喜欢吃甜食有影响 |
分析 根据观测值与对照临界值的关系,即可得出结论.
解答 解:根据观测值K2=10,对照临界值表得10>7.879,
所以有99.5%的把握认为性别对喜欢吃甜食有影响.
故选:B.
点评 本题考查了独立性检验的应用问题,是基础题.

练习册系列答案
相关题目
2.将函数y=sin(2x-$\frac{π}{6}$)的图象向左平移$\frac{1}{6}$个最小正周期后,所得图象对应的函数解析式为( )
| A. | y=sin(2x+$\frac{π}{6}$) | B. | y=sin2x | C. | y=sin(2x+$\frac{π}{3}$) | D. | y=sin(2x-$\frac{π}{3}$) |
6.已知随机变量ξ服从正态分布N(2,σ2),若P(0≤ξ≤2)=0.3,则P(ξ≥4)=( )
| A. | 0.2 | B. | 0.3 | C. | 0.6 | D. | 0.8 |
16.已知三棱锥S-ABC的各顶点都在一个球面上,△ABC所在截面圆的圆心O在AB上,SO⊥平面$ABC,AC=\sqrt{3},BC=1$,若三棱锥的体积是$\frac{{\sqrt{3}}}{3}$,则球体的表面积是( )
| A. | $\frac{25}{4}π$ | B. | $\frac{25}{12}π$ | C. | $\frac{125}{48}π$ | D. | 25π |
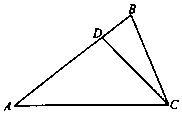 如图,在△ABC中,已知点D在边AB上,AD=3DB,cosA=$\frac{4}{5}$,cos∠ACB=$\frac{5}{13}$,BC=13.
如图,在△ABC中,已知点D在边AB上,AD=3DB,cosA=$\frac{4}{5}$,cos∠ACB=$\frac{5}{13}$,BC=13.