题目内容
6.已知f(x)是定义在R上的函数,其导函数为f'(x),若2f(x)-f'(x)<2,f(0)=2018,则不等式f(x)>2017e2x+1(其中e为自然对数的底数)的解集为(0,+∞).分析 构造函数g(x)=e-2xf(x)-e-2x,则g′(x)>0,g(x)单调递增,不等式f(x)>2017e2x+1两边同乘e-2x得出g(x)>2017,从而得出x的范围.
解答 解:设g(x)=e-2xf(x)-e-2x,
则g′(x)=-2e-2xf(x)+e-2xf′(x)+2e-2x=-e-2x[2f(x)-f′(x)-2],
∵2f(x)-f'(x)<2,
∴g′(x)>0,∴g(x)在R上单调递增.
∵f(x)>2017e2x+1,∴e-2xf(x)>2017+e-2x,即g(x)>2017,
∵g(0)=f(0)-1=2017,
∴x>0.
故答案为(0,+∞).
点评 本题考查了导数与函数单调性的关系,函数单调性的应用,构造g(x)是解题关键,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知Sn为等差数列{an}的前n项和.若S9=18,则a3+a5+a7=( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
14.已知i是虚数单位,若(1-i)(a+i)=3-bi(a,b∈R),则a+b等于( )
| A. | 3 | B. | 1 | C. | 0 | D. | -2 |
16.已知三棱锥S-ABC的各顶点都在一个球面上,△ABC所在截面圆的圆心O在AB上,SO⊥平面$ABC,AC=\sqrt{3},BC=1$,若三棱锥的体积是$\frac{{\sqrt{3}}}{3}$,则球体的表面积是( )
| A. | $\frac{25}{4}π$ | B. | $\frac{25}{12}π$ | C. | $\frac{125}{48}π$ | D. | 25π |
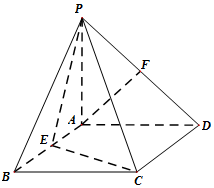 如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E,F分别是AB,PD的中点,且PA=AD.
如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E,F分别是AB,PD的中点,且PA=AD.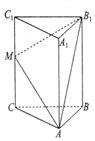 如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=BC=5,AB=6,M是CC1中点,CC1=8.
如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=BC=5,AB=6,M是CC1中点,CC1=8.