题目内容
9.已知集合A={x∈Z|x2-4x-5<0},B={x|4x>2m},若A∩B有三个元素,则实数m的取值范围是( )| A. | [3,6) | B. | [1,2) | C. | [2,4) | D. | (2,4] |
分析 分别求出集合A和B,根据A∩B有三个元素,能求出实数m的取值范围.
解答 解:∵集合A={x∈Z|x2-4x-5<0}={0,1,2,3,4},
B={x|4x>2m}={x|x>$\frac{m}{2}$},
∵A∩B有三个元素,
∴$1≤\frac{m}{2}<2$,解得2≤m<4,
∴实数m的取值范围是[2,4).
故选:C.
点评 本题考查交集的求法及应用,是基础题,解题时要认真审题,注意交集定义的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.从集合{2,3,4,5}中随机抽取一个数a,从集合{4,6,8}中随机抽取一个数b,则向量$\overrightarrow{m}$=(a,b)与向量$\overrightarrow{n}$=(-2,1)垂直的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
20.已知向量$\overrightarrow{a}$=(x,1),$\overrightarrow{b}$=(3,-2),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则x=( )
| A. | -3 | B. | $-\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
14.已知i是虚数单位,若(1-i)(a+i)=3-bi(a,b∈R),则a+b等于( )
| A. | 3 | B. | 1 | C. | 0 | D. | -2 |
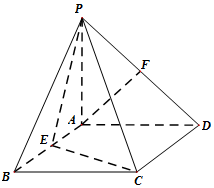 如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E,F分别是AB,PD的中点,且PA=AD.
如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E,F分别是AB,PD的中点,且PA=AD.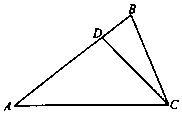 如图,在△ABC中,已知点D在边AB上,AD=3DB,cosA=$\frac{4}{5}$,cos∠ACB=$\frac{5}{13}$,BC=13.
如图,在△ABC中,已知点D在边AB上,AD=3DB,cosA=$\frac{4}{5}$,cos∠ACB=$\frac{5}{13}$,BC=13.