题目内容
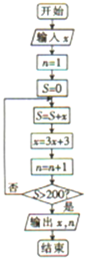
如图是某种算法的程序框图，若输入x=2，则输出的x，n分别为（ ）
| A、x=282，n=4 |
| B、x=282，n=5 |
| C、x=849，n=5 |
| D、x=849，n=6 |
考点：程序框图
专题：算法和程序框图
分析：模拟执行程序框图，依次写出每次循环得到的S，x，n的值，当S=134+282=416＞200，退出循环，输出x=849，n=6．
解答：
解：模拟执行程序框图，可得
第1步：S=2，x=3×2+3=9，n=2；
第2步：S=2+9=11，x=3×9+3=30，n=3；
第3步：S=11+30=41，x=3×30+3=93，n=4；
第4步：S=41+93=134，x=3×93+3=282，n=5；
第5步：S=134+282=416＞200，x=849，n=6；
所以输出的x=849，n=6．
故选：D．
第1步：S=2，x=3×2+3=9，n=2；
第2步：S=2+9=11，x=3×9+3=30，n=3；
第3步：S=11+30=41，x=3×30+3=93，n=4；
第4步：S=41+93=134，x=3×93+3=282，n=5；
第5步：S=134+282=416＞200，x=849，n=6；
所以输出的x=849，n=6．
故选：D．
点评：本题主要考查了程序框图和算法，正确写出每次循环得到的S，x，n的值是解题的关键，属于基础题．
练习册系列答案
相关题目
12件同类产品中，有10件是正品，2件是次品，从中任意抽出3件，与“抽得1件次品2件正品”互斥而不对立的事件是（ ）
| A、抽得3件正品 |
| B、抽得至少有1件正品 |
| C、抽得至少有1件次品 |
| D、抽得3件正品或2件次品1件正品 |
经过直线2x-y=0与直线x+y-6=0的交点，且与直线2x+y-1=0平行的直线方程是（ ）
| A、x-2y+6=0 |
| B、x-2y-6=0 |
| C、2x+y-8=0 |
| D、x+2y+8=0 |
由下列各组命题构成“p或q”“p且q”“非p”形式的命题中，“p或q”为真，“p且q”为假，“非p”为真的是（ ）
| A、p：3是偶数；q：4是奇数 | ||
| B、p：3+2=6；q：5＞3 | ||
| C、p：a∈{a，b}；q：{a}⊆{a，b} | ||
D、p：y2=x的焦点到准线的距离为
|
设集合U={1，2，3，4，5，6}，A={1，2，3}，B={2，5}，则（∁UA）∩（∁UB）=（ ）
| A、{2，3，6} |
| B、{4，6} |
| C、{3，6} |
| D、{5，6} |