题目内容
经过直线2x-y=0与直线x+y-6=0的交点,且与直线2x+y-1=0平行的直线方程是( )
| A、x-2y+6=0 |
| B、x-2y-6=0 |
| C、2x+y-8=0 |
| D、x+2y+8=0 |
考点:直线的一般式方程与直线的平行关系
专题:直线与圆
分析:联立两直线方程求得交点坐标,由题意设出经过直线2x-y=0与直线x+y-6=0的交点,且与直线2x+y-1=0平行的直线方程为2x+y=m,代入交点坐标求出m的值得答案.
解答:
解:联立
,解得
.
∴直线2x-y=0与直线x+y-6=0的交点为(2,4),
设与直线2x+y-1=0平行的直线方程是2x+y=m,
∵(2,4)在直线2x+y=m上,
∴2×2+4=m,即m=8.
∴经过直线2x-y=0与直线x+y-6=0的交点,且与直线2x+y-1=0平行的直线方程是2x+y-8=0.
故选:C.
|
|
∴直线2x-y=0与直线x+y-6=0的交点为(2,4),
设与直线2x+y-1=0平行的直线方程是2x+y=m,
∵(2,4)在直线2x+y=m上,
∴2×2+4=m,即m=8.
∴经过直线2x-y=0与直线x+y-6=0的交点,且与直线2x+y-1=0平行的直线方程是2x+y-8=0.
故选:C.
点评:本题考查了直线的一般式方程与直线平行的关系,考查了两直线的交点坐标的求法,是基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
如图是某种算法的程序框图,若输入x=2,则输出的x,n分别为( )
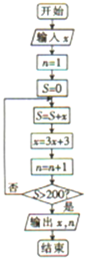

| A、x=282,n=4 |
| B、x=282,n=5 |
| C、x=849,n=5 |
| D、x=849,n=6 |
偶函数f(x)的定义域为R,当x∈[0,+∞)时,f(x)是增函数,则不等式f(x)>f(1)的解集是( )
| A、(1,+∞) | ||
| B、(-∞,-1)∪(1,+∞). | ||
C、(-∞,
| ||
D、(
|
“x>3”是“x2>9”的.( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
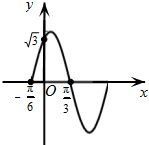 如图,函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,0≤φ≤
如图,函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,0≤φ≤