题目内容
11.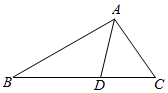 如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,cos∠C=$\frac{3}{5}$.
如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,cos∠C=$\frac{3}{5}$.(Ⅰ)求sin∠ADB的值;
(Ⅱ)若BD=2DC=5,求△ABD的面积.
分析 (I)求出sinC,则sin∠ADB=sin∠ADC=sin(C+∠CAD);
(II)在△ACD中使用正弦定理计算AD,代入三角形的面积公式S△ABD=$\frac{1}{2}AD•BD•sin∠ADB$即可.
解答 解:(I)在△ABC中,∵cosC=$\frac{3}{5}$,∴sinC=$\frac{4}{5}$.
∴sin∠ADC=sin(C+∠CAD)=sinCcos∠CAD+cosCsin∠CAD=$\frac{4}{5}×\frac{\sqrt{2}}{2}+\frac{3}{5}×\frac{\sqrt{2}}{2}=\frac{7\sqrt{2}}{10}$.
∵∠ADB+∠ADC=π,
∴sin∠ADB=sin∠ADC=$\frac{7\sqrt{2}}{10}$.
(II)在△ACD中,由正弦定理得$\frac{CD}{sin∠CAD}=\frac{AD}{sinC}$,
∴$\frac{\frac{5}{2}}{\frac{\sqrt{2}}{2}}=\frac{AD}{\frac{4}{5}}$,解得AD=2$\sqrt{2}$.
∴S△ABD=$\frac{1}{2}AD•BD•sin∠ADB$=$\frac{1}{2}×5×2\sqrt{2}×\frac{7\sqrt{2}}{10}$=7.
点评 本题考查了两角和的正弦公式,正弦定理,三角形的面积计算,属于中档题.

练习册系列答案
相关题目
1.下列命题中错误的是( )
| A. | 圆柱的轴截面是过母线的截面中面积最大的一个 | |
| B. | 圆锥的轴截面是所在过顶点的截面中面积最大的一个 | |
| C. | 圆台的所有平行于底面的截面都是圆面 | |
| D. | 圆锥所有的轴截面是全等的等腰三角形 |
6.在矩形ABCD中,AB=2,AD=1,点P为矩形ABCD内一点,则使得$\overrightarrow{AP}$•$\overrightarrow{AC}$≥1的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |
3.为了得到函数的图象y=sin(3x+1),只需把函数y=sin3x的图象上所有的点( )
| A. | 向左平移1个单位长度 | B. | 向右平移1个单位长度 | ||
| C. | 向左平移$\frac{1}{3}$个单位长度 | D. | 向右平移$\frac{1}{3}$个单位长度 |
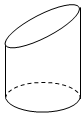 用一个不平行于底面的平面截一个底面直径为6cm的圆柱,得到如图几何体,若截面椭圆的长轴长为10cm,这个几何体最短的母线长为6cm,则此几何体的体积为90πcm3.
用一个不平行于底面的平面截一个底面直径为6cm的圆柱,得到如图几何体,若截面椭圆的长轴长为10cm,这个几何体最短的母线长为6cm,则此几何体的体积为90πcm3.