题目内容
2．
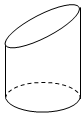用一个不平行于底面的平面截一个底面直径为6cm的圆柱，得到如图几何体，若截面椭圆的长轴长为10cm，这个几何体最短的母线长为6cm，则此几何体的体积为90πcm3．
分析 过最短母线的端点向最长母线作垂线，利用勾股定理计算最长母线的高度，将两个相同的几何体拼接成一个圆柱体计算体积．
解答 
解：过最短母线的端点向最长母线作垂线AB，设最长母线的顶端为C，连结AC．
则AB=6，AC=10，∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}=8$．
∴两个相同的几何体可以拼接成一个底面直径为6cm，高为20cm的圆柱．
∴几何体的体积V=$\frac{1}{2}$π×32×20=90π．
故答案为：90π．
点评 本题考查了圆柱的结构特征，不规则几何体的体积计算，属于基础题．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
13．已知点P（1，$\sqrt{5}$）在双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的渐近线上，则该双曲线的离心率为（ ）
| A． | $\sqrt{3}$ | B． | 2 | C． | $\sqrt{5}$ | D． | $\sqrt{6}$ |
10．
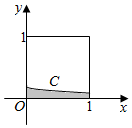在如图所示的正方形中随机投掷10000个点，则落入阴影部分（曲线C为正态分布N（-2，1）的密度曲线）的点的个数的估计值为（ ）
[附：若X～N（μ，σ2），则P（μ-σ＜X＜μ+σ）=0.6826，
P（μ-2σ＜X＜μ+2σ）=0.9544，
P（μ-3σ＜X＜μ+3σ）=0.9974]．
在如图所示的正方形中随机投掷10000个点，则落入阴影部分（曲线C为正态分布N（-2，1）的密度曲线）的点的个数的估计值为（ ）[附：若X～N（μ，σ2），则P（μ-σ＜X＜μ+σ）=0.6826，
P（μ-2σ＜X＜μ+2σ）=0.9544，
P（μ-3σ＜X＜μ+3σ）=0.9974]．
| A． | 430 | B． | 215 | C． | 2718 | D． | 1359 |
14．设I={（x，y）|x∈R且y∈R}，P，Q均为I的子集，定义Q○P={（x，z）|存在y使（x，y）∈P且（y，z）∈Q}，已知X，Y，Z为I的子集，下列正确的是（ ）
| A． | （X∪Y）○Z=（X○Z）∩（Y○Z） | B． | （X∩Y）○Z=（X○Z）∪（Y○Z） | C． | （X∪Y）○Z=（X○Z）∪（Y○Z） | D． | （X∩Y）○Z=（X○Z）∩（Y○Z） |
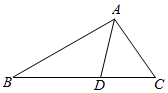如图，在△ABC中，点D在BC边上，∠CAD=$\frac{π}{4}$，cos∠C=$\frac{3}{5}$．