题目内容
6.在矩形ABCD中,AB=2,AD=1,点P为矩形ABCD内一点,则使得$\overrightarrow{AP}$•$\overrightarrow{AC}$≥1的概率为( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |
分析 将矩形放在坐标系中,设P(x,y)利用向量的数量积公式,作出对应的区域,求出对应的面积即可得到结论.
解答 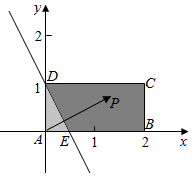 解:将矩形放在坐标系中,设P(x,y),
解:将矩形放在坐标系中,设P(x,y),
则A(0,0),C(2,1),
则$\overrightarrow{AP}$•$\overrightarrow{AC}$≥1等价为2x+y≥1,
作出不等式对应的区域,为五边形DCBE,
当y=0时,x=$\frac{1}{2}$,即E($\frac{1}{2}$,0),
则△ADE的面积S=$\frac{1}{2}×\frac{1}{2}×1$=$\frac{1}{4}$,
则五边形DCBE的面积S=2-$\frac{1}{4}$=$\frac{7}{4}$
则$\overrightarrow{AP}$•$\overrightarrow{AC}$≥1的概率P=$\frac{\frac{7}{4}}{2}$=$\frac{7}{8}$,
故选:D.
点评 本题主要考查几何概型的概率的计算,根据向量数量积的坐标关系,求出对应区域面积,是解决本题的关键.

练习册系列答案
相关题目
14.设I={(x,y)|x∈R且y∈R},P,Q均为I的子集,定义Q○P={(x,z)|存在y使(x,y)∈P且(y,z)∈Q},已知X,Y,Z为I的子集,下列正确的是( )
| A. | (X∪Y)○Z=(X○Z)∩(Y○Z) | B. | (X∩Y)○Z=(X○Z)∪(Y○Z) | C. | (X∪Y)○Z=(X○Z)∪(Y○Z) | D. | (X∩Y)○Z=(X○Z)∩(Y○Z) |
15.在△ABC中,∠C=90°,$\overrightarrow{BA}$=(k,1),$\overrightarrow{BC}$=(2,3),则k的值是( )
| A. | 5 | B. | -5 | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
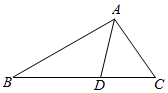 如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,cos∠C=$\frac{3}{5}$.
如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,cos∠C=$\frac{3}{5}$.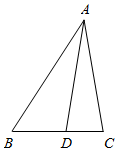 在△ABC中,角A,B,C的对应边分别为a,b,c,且三角形的面积为S=$\frac{{\sqrt{3}}}{2}$accosB.
在△ABC中,角A,B,C的对应边分别为a,b,c,且三角形的面积为S=$\frac{{\sqrt{3}}}{2}$accosB.