题目内容
已知函数f(x)=
sin2x•sinφ+cos2x•cosφ+
sin(
π-φ)(0<φ<π),其图象过点(
,
.)
(Ⅰ)求函数f(x)在[0,π]上的单调递减区间;
(Ⅱ)若x0∈(
,π),sinx0=
,求f(x0)的值.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
(Ⅰ)求函数f(x)在[0,π]上的单调递减区间;
(Ⅱ)若x0∈(
| π |
| 2 |
| 3 |
| 5 |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的求值,三角函数的图像与性质
分析:(Ⅰ)首先根据三角函数的恒等变换把函数关系式变形成正弦型函数,进一步求出函数的单调区间.
(Ⅱ)首先根据(Ⅰ)的结果求出三角函数的正弦值和余弦值进一步求出结果.
(Ⅱ)首先根据(Ⅰ)的结果求出三角函数的正弦值和余弦值进一步求出结果.
解答:
(本小题满分12分)φ
解:(Ⅰ)f(x)=
sin2x•sinφ+
(1+cos2x)cosφ-
cosφ
=
sin2x•sinφ+
cos2x•cosφ
=
cos(2x-φ)
由f(x)图象过点(
,
)知:
cos(
-φ)=1(0<φ<π)
所以:φ=
所以f(x)=
cos(2x-
)
令2kπ≤2x-
≤2kπ+π(k∈Z)
即:kπ+
≤x≤kπ+
所以:函数f(x)在[0,π]上的单调区间为:[
,
]
(Ⅱ)因为x0∈(π,2π),sinx0=
则:cosx0=-
2x0∈(π,2π)
则:cos2x0=cos2x0-sin2x0=
sin2x0=-
所以f(x0)=
cos(2x0-
)=
(cos2x0cos
+sin2x0sin
)=
解:(Ⅰ)f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
由f(x)图象过点(
| π |
| 6 |
| 1 |
| 2 |
cos(
| π |
| 3 |
所以:φ=
| π |
| 3 |
所以f(x)=
| 1 |
| 2 |
| π |
| 3 |
令2kπ≤2x-
| π |
| 3 |
即:kπ+
| π |
| 6 |
| 2π |
| 3 |
所以:函数f(x)在[0,π]上的单调区间为:[
| π |
| 6 |
| 2π |
| 3 |
(Ⅱ)因为x0∈(π,2π),sinx0=
| 3 |
| 5 |
则:cosx0=-
| 4 |
| 5 |
2x0∈(π,2π)
则:cos2x0=cos2x0-sin2x0=
| 7 |
| 25 |
sin2x0=-
| 24 |
| 25 |
所以f(x0)=
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
7-24
| ||
| 100 |
点评:本题考查的知识要点:三角函数关系式的恒等变换,正弦型函数单调区间的确定,三角函数的求值问题,属于基础题型.

练习册系列答案
相关题目
若A、B为锐角△ABC的两个锐角,函数f(x)在(0,1)上是单减函数,则( )
| A、f(sinA)>f(cosB) |
| B、f(sinA)<f(cosB) |
| C、f(cosA)=f(sinB) |
| D、f(cosA)>f(sinB) |
已知正方形ABCD的边长为2,P是平面ABCD外一点,且PA=PB=PC=PD=2
,则PA与平面ABCD所成的角是( )
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
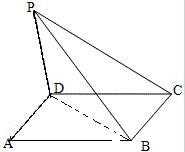 如图,PD⊥平面ABCD,AD⊥PC,AD∥BC,PD:DC:BC=1:1:
如图,PD⊥平面ABCD,AD⊥PC,AD∥BC,PD:DC:BC=1:1: