题目内容
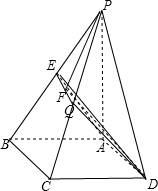
 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,且PB与底面ABCD所成的角为45°,E为PB的中点,过A,E,D三点的平面记为α,PC与α的交点为Q.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,且PB与底面ABCD所成的角为45°,E为PB的中点,过A,E,D三点的平面记为α,PC与α的交点为Q.(Ⅰ)试确定Q的位置并证明;
(Ⅱ)求四棱锥P-ABCD被平面α分成上下两部分的体积比.
(Ⅲ)若PA=2,截面AEQD的面积为3,求平面α与平面PCD所成的二面角的正切值.
考点:二面角的平面角及求法,棱柱、棱锥、棱台的体积
专题:
分析:(Ⅰ)利用线面平行和线线平行之间的转化求出结论.
(Ⅱ)利用线面的垂直,进一步算出锥体的体积运算求出比值.
(Ⅲ)通过做出二面角的平面角求出相关的量,进一步解直角三角形求得结果.
(Ⅱ)利用线面的垂直,进一步算出锥体的体积运算求出比值.
(Ⅲ)通过做出二面角的平面角求出相关的量,进一步解直角三角形求得结果.
解答:
 解:(Ⅰ)Q为PC的中点.
解:(Ⅰ)Q为PC的中点.
理由证明如下:因为AD∥BC,AB?平面PBC,故AD∥平面PBC.
又由于平面α∩平面PBC=EQ,故AD∥EQ.
所以:BC∥EQ.
又E为PB的中点,故Q为PC的中点.
(Ⅱ)如图连接EQ,DQ,
因为:PA⊥平面ABCD,所以PB与平面ABCD所成的角为∠PBA=45°
故:PA=AB
又因为:E为PB的中点,
所以PE⊥AE.
因为四边形ABCD是矩形,所以AD⊥AB.
又PA⊥平面ABCD
得到:AD⊥PA,又PA∩AB=A
故:PE⊥平面α
设:PA=h,AD=2a,四棱锥P-ABCD被平面α所分成的上下两部分分别为V1和V2
则:EQ=a
又因为AD⊥平面PAB,所以AD⊥AE.
V上=
•PE•SAEQD=
h•
(a+2a)
h=
h2
V下=
PA•SABCD-V上=
ah2
=
(Ⅲ)过E作EF⊥DQ,连接PF,
因为PE⊥平面α,所以PE⊥DF
又由于EF∩PE=E,所以DF⊥平面PEF,
则:DF⊥PF
所以:∠PFE是平面α和平面PCD所成的二面角.
因为:PA=2,即h=2,截面AEQD的面积为3.
所以:SAEQD=
(a+2a)
h=3
解得:a=
又因为:AD∥EQ,且EQ=
AD,
故:S△EQD=
SAEQD=1
QD=
=2
又S△EQD=
EF•DQ=1
解得:EF=1.
PE=
PB=
在直角三角形PEF中,tan∠PFE=
=
即:平面α与平面PCD所成的二面角的正切值为
.
 解:(Ⅰ)Q为PC的中点.
解:(Ⅰ)Q为PC的中点.理由证明如下:因为AD∥BC,AB?平面PBC,故AD∥平面PBC.
又由于平面α∩平面PBC=EQ,故AD∥EQ.
所以:BC∥EQ.
又E为PB的中点,故Q为PC的中点.
(Ⅱ)如图连接EQ,DQ,
因为:PA⊥平面ABCD,所以PB与平面ABCD所成的角为∠PBA=45°
故:PA=AB
又因为:E为PB的中点,
所以PE⊥AE.
因为四边形ABCD是矩形,所以AD⊥AB.
又PA⊥平面ABCD
得到:AD⊥PA,又PA∩AB=A
故:PE⊥平面α
设:PA=h,AD=2a,四棱锥P-ABCD被平面α所分成的上下两部分分别为V1和V2
则:EQ=a
又因为AD⊥平面PAB,所以AD⊥AE.
V上=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| a |
| 4 |
V下=
| 1 |
| 3 |
| 5 |
| 12 |
| V上 |
| V下 |
| 3 |
| 5 |
(Ⅲ)过E作EF⊥DQ,连接PF,
因为PE⊥平面α,所以PE⊥DF
又由于EF∩PE=E,所以DF⊥平面PEF,
则:DF⊥PF
所以:∠PFE是平面α和平面PCD所成的二面角.
因为:PA=2,即h=2,截面AEQD的面积为3.
所以:SAEQD=
| 1 |
| 2 |
| ||
| 2 |
解得:a=
| 2 |
又因为:AD∥EQ,且EQ=
| 1 |
| 2 |
故:S△EQD=
| 1 |
| 3 |
QD=
| (AD-QE)2+AE2 |
又S△EQD=
| 1 |
| 2 |
解得:EF=1.
PE=
| 1 |
| 2 |
| 2 |
在直角三角形PEF中,tan∠PFE=
| PE |
| EF |
| 2 |
即:平面α与平面PCD所成的二面角的正切值为
| 2 |
点评:本题考查的知识要点:线面的垂直和平行问题,锥体的体积,二面角的平面角的应用.属于中等题型.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
在△ABC中,|
|=3,|
|=2,点D满足2
=3
,∠BAC=60°,则
•
=( )
| AB |
| AC |
| BD |
| DC |
| AD |
| BC |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
