题目内容
四面体ABCD中，∠ACB=30°，∠DCB=45°，∠ACD=60°，设二面角A-BC-D的平面角为α，则cosα= ．
考点：二面角的平面角及求法
专题：空间角
分析：由题意，作AO⊥平面BCD，垂足为O，作OE⊥BC，交BC于E，连结AE，则∠AEO=α，由此利用余弦定理能求出cosα=
-
．
| 2 |
| 3 |
解答：
解：由题意，作AO⊥平面BCD，垂足为O，作OE⊥BC，交BC于E，连结AE，
则∠AEO=α，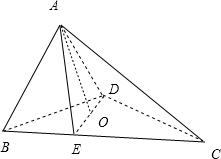
∵DC的长度不影响∠α的大小，
∴使得E、O、D共线，
设AE=a，
=∠ACE=30°，∴AC=2a，EC=
a，
又∵∠DCE=45°，DE⊥BC，
∴DE=
a，DC=
a，
又∵∠ACD=60°，
∴cos∠ACD=
=
=
，
解得AD2=（10-2
）a2，
∴cos∠AED=
=
=
-
．
∴cosα=
-
．
故答案为：
-
．
则∠AEO=α，
∵DC的长度不影响∠α的大小，
∴使得E、O、D共线，
设AE=a，
=∠ACE=30°，∴AC=2a，EC=
| 3 |
又∵∠DCE=45°，DE⊥BC，
∴DE=
| 3 |
| 6 |
又∵∠ACD=60°，
∴cos∠ACD=
| AC2+CD2-AD2 |
| 2AC•CD |
| 4a2+6a2-AD2 | ||
2×2a×
|
| 1 |
| 2 |
解得AD2=（10-2
| 6 |
∴cos∠AED=
| AE2+ED2-AD2 |
| 2AE•ED |
a2+3a2-(10-2
| ||
2
|
| 2 |
| 3 |
∴cosα=
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：本题考查二面角的余弦值的求法，是中档题，解题时要注意余弦定理的合理运用．
练习册系列答案
相关题目
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，且PB与底面ABCD所成的角为45°，E为PB的中点，过A，E，D三点的平面记为α，PC与α的交点为Q．
如图所示，四棱锥P-ABCD，底面四边形ABCD是正方形，侧面PCD是边长为a的正三角形，且平面PCD⊥底面ABCD，E为PC的中点．