题目内容
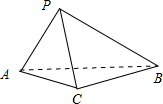 如图,已知四面体PABC的四个顶点P,A,B,C均在球O的表面上,且AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC,则球O的体积是
如图,已知四面体PABC的四个顶点P,A,B,C均在球O的表面上,且AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC,则球O的体积是考点:球的体积和表面积
专题:空间位置关系与距离
分析:如图所示,取AB的中点D,过点D作OD⊥平面ABC,由于PC⊥AC,AC=BC,PA=PB,可得PC⊥BC,PC⊥平面ABC.设OD交PC的垂直平分线于点O,则点O为球心.求出即可.
解答:
解:如图所示,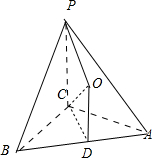
取AB的中点D,过点D作OD⊥平面ABC,
∵PC⊥AC,AC=BC,PA=PB,
∴PC⊥BC,
又AC∩BC=C,
∴PC⊥平面ABC.
∴PC∥OD.
OD交PC的垂直平分线于点O,则点O为球心.
球的半径R=OC=
=
=
.
∴球O的体积V=
R3=
=4
π.
故答案为:4
π.

取AB的中点D,过点D作OD⊥平面ABC,
∵PC⊥AC,AC=BC,PA=PB,
∴PC⊥BC,
又AC∩BC=C,
∴PC⊥平面ABC.
∴PC∥OD.
OD交PC的垂直平分线于点O,则点O为球心.
球的半径R=OC=
CD2+(
|
(
|
| 3 |
∴球O的体积V=
| 4π |
| 3 |
4π×(
| ||
| 3 |
| 3 |
故答案为:4
| 3 |
点评:本题考查了线面垂直的判定与性质、勾股定理、球的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
某四面体的三视图如图所示,三个三角形均为直角三角形,则该四面体的表面积是( )
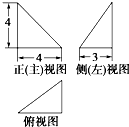

| A、8 | ||
B、22+2
| ||
C、18+6
| ||
D、24+6
|